题目内容
12.为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:| 收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
分析 由题意可得$\overline{x}$和$\overline{y}$,可得回归方程,把x=15代入方程求得y值即可.
解答 解:由题意可得$\overline{x}$=$\frac{1}{5}$(8.2+8.6+10.0+11.3+11.9)=10,
$\overline{y}$=$\frac{1}{5}$(6.2+7.5+8.0+8.5+9.8)=8,
代入回归方程可得a=8-0.76×10=0.4,
∴回归方程为y=0.76x+0.4,
把x=15代入方程可得y=0.76×15+0.4=11.8,
故答案为:11.8.
点评 本题考查线性回归方程,涉及平均值的计算,属基础题.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
3.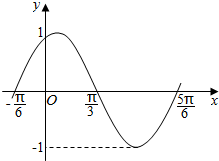 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象如图所示,为了得到这个函数的图象,只需将y=sinx(x∈R)的图象上的所有的点( )| A. | 向左平移$\frac{π}{6}$个长度单位,再把所得各点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| B. | 向左平移$\frac{π}{3}$个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变 | |
| C. | 向左平移$\frac{π}{3}$个长度单位,再把所得各点的横坐标变为原来的$\frac{1}{2}$倍,纵坐标不变 | |
| D. | 向左平移$\frac{π}{6}$个长度单位,再把所得各点的横坐标变为原来的2倍,纵坐标不变 |
7.用斜二测画法作出一个三角形的直观图,则原三角形面积是直观图面积的( )
| A. | $\frac{1}{2}$倍 | B. | 2$\sqrt{2}$倍 | C. | 2倍 | D. | $\frac{\sqrt{2}}{4}$倍 |
4.函数f(x)=x+$\frac{1}{x}$(x>0)的最小值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
1.已知函数$f(x)={log_a}({x^2}+2x-3)$,若f(2)<0,则此函数的单调递增区间是( )
| A. | (1,+∞)∪(-∞,-3) | B. | (1,+∞) | C. | (-∞,-1) | D. | (-∞,-3) |
2.函数$y=lg(\frac{2}{x+1}-1)$的图象关于( )
| A. | x轴成轴对称图形 | B. | y轴成轴对称图形 | ||
| C. | 原点成中心对称图形 | D. | 直线y=x成轴对称图形 |