题目内容
20.已知样本数据x1,x2,…,xn的方差为5,则样本数据2x1+1,2x2+1,…,2xn+1的方差为20.分析 先根据方差的性质,计算出样本2x1、2x2、…、2xn的方差,然后再求样本2x1+1、2x2+1、…、2xn+1的方差即可.
解答 解:∵样本x1、x2、…、xn的方差为5,
又∵一组数据中的各个数据都扩大几倍,则新数据的方差扩大其平方倍,
∴样本2x1、2x2、…、2xn的方差为22×5=20,
∵一组数据中的各个数据都加上同一个数后得到的新数据的方差与原数据的方差相等,
∴样本2x1+1、2x2+1、…、2xn+1的方差为20.
故答案为:20.
点评 本题考查方差的求法,是基础题,解题时要认真审题,注意方差性质的合理运用.

练习册系列答案
相关题目
5.在△ABC中,角A、B、C所对的对边长分别为a、b、c,sinA、sinB、sinC成等比数列,且c=2a,则cosB的值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{4}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{2}}{3}$ |
12.为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
根据上表可得回归直线方程$\hat y=\hat bx+\hat a$,其中$\hat b=0.76$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,据此估计,该社区一户居民年收入为15万元家庭的年支出为11.8万元.
| 收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
9.以椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1内一点P(1,1)为中点的弦所在的直线方程是( )
| A. | 3x-4y+2=0 | B. | 3x+4y-7=0 | C. | 3x-4y+7=0 | D. | 3x-4y-2=0 |
 ,下列结论中不正确的是( )
,下列结论中不正确的是( )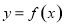 的图象关于点
的图象关于点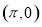 中心对称
中心对称 对称
对称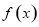 的最大值为
的最大值为
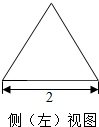 已知一个正三棱柱的所有棱长均相等,其侧(左)视图如图所示,那么此三棱柱正(主)视图的面积为$2\sqrt{3}$.表面积为$2\sqrt{3}$+12.体积为$2\sqrt{3}$.
已知一个正三棱柱的所有棱长均相等,其侧(左)视图如图所示,那么此三棱柱正(主)视图的面积为$2\sqrt{3}$.表面积为$2\sqrt{3}$+12.体积为$2\sqrt{3}$.