题目内容
2.求证:连续n个正整数的乘积是n!的倍数.分析 n个连续的正整数之积可表示为:S=k(k+1)(k+2)(k+3)…(k+n-1)=${A}_{k+n-1}^{n}$=${C}_{k+n-1}^{n}$•n!,命题得以证明.
解答 证明:不妨设这n个连续的正整数分别为:
k,k+1,k+2,k+3,…,k+n-1,(k,n∈N*),
它们的积记为S=k(k+1)(k+2)(k+3)…(k+n-1),
根据排列数公式,上式也可以写成:${A}_{k+n-1}^{n}$,
即S=${A}_{k+n-1}^{n}$,
再根据排列数和组合数之间的关系式,${A}_{m}^{n}$=${C}_{m}^{n}$•${A}_{n}^{n}$,
因此,${A}_{k+n-1}^{n}$=${C}_{k+n-1}^{n}$•${A}_{n}^{n}$,
所以,S=${A}_{k+n-1}^{n}$=${C}_{k+n-1}^{n}$•${A}_{n}^{n}$=${C}_{k+n-1}^{n}$•n!,
即k(k+1)(k+2)(k+3)…(k+n-1)=M•n!,
其中,M=${C}_{k+n-1}^{n}$∈N*,
所以,这连续n个正整数的乘积是n!的倍数.
点评 本题主要考查了整数中的整除问题,运用了构造法将问题转化为排列数与组合数的计算问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知直线y=kx-1和双曲线x2-y2=1的右支交于不同两点,则k的取值范围是( )
| A. | $({1,\sqrt{2}})$ | B. | $({-\sqrt{2},-1})∪({1,\sqrt{2}})$ | C. | $({-\sqrt{2},\sqrt{2}})$ | D. | $({-\sqrt{2},-1})∪({-1,1})∪({1,\sqrt{2}})$ |
12.为了解某社区居民的家庭年收入与年支出的关系,随机调查了该社区5户家庭,得到如下统计数据表:
根据上表可得回归直线方程$\hat y=\hat bx+\hat a$,其中$\hat b=0.76$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,据此估计,该社区一户居民年收入为15万元家庭的年支出为11.8万元.
| 收入x(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出y(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
 中,
中,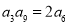 ,数列
,数列 是等差数列,且
是等差数列,且 ,则
,则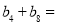 ( )
( ) 的焦点作两条垂直的弦
的焦点作两条垂直的弦 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 ,下列结论中不正确的是( )
,下列结论中不正确的是( )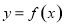 的图象关于点
的图象关于点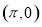 中心对称
中心对称 对称
对称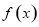 的最大值为
的最大值为
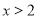 ”是“
”是“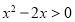 ”成立的必要条件
”成立的必要条件 ,则
,则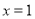 ”的逆否命题为假命题
”的逆否命题为假命题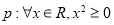 ”的否定形式为“
”的否定形式为“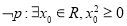 ”
”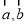 ,则“
,则“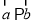 ”是“
”是“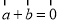 ” 的充要条件
” 的充要条件