题目内容
判断函数y=
的奇偶性．
| tan2x-tanx |
| 1-tanx |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：首先，确定函数的定义域，然后，化简函数解析式，最后，结合函数的奇偶性的概念进行判断．
解答：
解：函数为奇函数，证明如下：
∵1-tanx≠0，
∴tanx≠1，
∴x≠
+kπ，（k∈Z），
∴函数的定义域{x|x≠
+kπ，k∈Z}，
∵它不关于原点对称，
∴函数为非奇非偶函数．
∵1-tanx≠0，
∴tanx≠1，
∴x≠
| π |
| 4 |
∴函数的定义域{x|x≠
| π |
| 4 |
∵它不关于原点对称，
∴函数为非奇非偶函数．
点评：本题重点考查了函数的定义域求解方法，函数奇偶性的判断等知识，属于基础题．本题容易出现的问题是：遗漏函数的定义域问题．
练习册系列答案
阅读快车系列答案
相关题目
命题“若α=
，则tanα=1”的逆否命题是（ ）
| π |
| 4 |
A、若α≠
| ||
B、若tanα≠1，则α≠
| ||
C、若α=
| ||
D、若tanα≠1，则α=
|
已知直线l1：x+ay+1=0，直线l2：ax+y+2=0，则命题“若a=1或a=-1，则直线l1与l2平行”的否命题为（ ）
| A、若a≠1且a≠-1，则直线l1与l2不平行 |
| B、若a≠1或a≠-1，则直线l1与l2不平行 |
| C、若a=1或a=-1，则直线l1与l2不平行 |
| D、若a≠1或a≠-1，则直线l1与l2平行 |
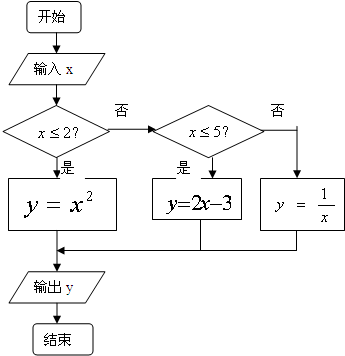如图：