题目内容
12.已知a>0,设命题p:函数 y=logax 在R上单调递增;命题q:不等式ax2-ax+1>0对?x∈R恒成立.若p且q为假,p或q为真,求a的取值范围.
分析 对于命题p:利用指数函数单调性可得:a>1.对于命题q:a=0(舍去),或a>0且△<0.由“p∧q”为假,“p∨q”为真,可得p、q中必有一真一假.
解答 解:对于命题p:∵函数y=ax在R上单调递增,∴a>1.
对于命题q:不等式ax2-ax+1>0对?x∈R恒成立,∴a=0(舍去),或a>0且△=a2-4a<0,解得0<a<4.
∴0<a<4.
∵“p∧q”为假,“p∨q”为真,
∴p、q中必有一真一假.
①当p真,q假时,$\left\{\begin{array}{l}{a>1}\\{a≥4}\end{array}\right.$,得a≥4.
②当p假,q真时,$\left\{\begin{array}{l}{0<a≤1}\\{0<a<4}\end{array}\right.$,得0<a≤1.
故a的取值范围为(0,1]∪[4,+∞).
点评 本题考查了复合命题真假的判定方法、指数函数的单调性、一元二次不等式的解集与判别式的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
2.定义在(0,π)上的函数f(π-x)=f(x),对任意x$∈(0,\frac{π}{2})$,不等式f(x)-f′(x)tanx>0恒成立,则下列不等式成立的是( )
| A. | $\sqrt{6}$f($\frac{π}{6}$)$<\sqrt{3}$f($\frac{π}{4}$)$<\sqrt{2}$f($\frac{2π}{3}$) | B. | $\sqrt{6}$f($\frac{π}{6}$)$<\sqrt{2}$f($\frac{2π}{3}$)$<\sqrt{3}$f($\frac{π}{4}$) | C. | $\sqrt{2}$f($\frac{2π}{3}$)$<\sqrt{3}$f($\frac{π}{4}$)<$\sqrt{6}$f($\frac{π}{6}$) | D. | $\sqrt{3}$f($\frac{π}{4}$)<$\sqrt{6}$f($\frac{π}{6}$)$\sqrt{2}$f($\frac{2π}{3}$) |
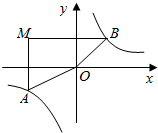 如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.
如图,在平面直角坐标系中,过点M(-3,2)分别作x轴、y轴的垂线与反比例函数$y=\frac{4}{x}$的图象交于A、B两点,则四边形MAOB的面积为10.