题目内容
 正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=
正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=
| ||
| 2 |
(1)AC⊥BE;
(2)EF∥平面ABCD;
(3)面AEF⊥面BEF;
(4)三棱锥A-BEF的体积为定值.
考点:棱柱的结构特征
专题:计算题,空间位置关系与距离
分析:通过直线AC垂直平面平面BB1D1D,判断(1)是正确的;通过直线EF平行直线DB,判断EF∥平面ABCD,(2)是正确的;对角面与侧面所成角为45°,故面AEF与面BEF不可能垂直;计算三角形BEF的面积和A到平面BEF的距离是定值,说明(4)是正确的.
解答:
解:∵AC⊥平面BB1D1D,又BE?平面BB1D1D∴AC⊥BE.故(1)正确;
∵B1D1∥平面ABCD,又E、F在直线D1B1上运动,∴EF∥平面ABCD.故(2)正确;
∵对角面与侧面所成角为45°,∴面AEF与面BEF不可能垂直,故(3)不正确;
(4)中由于点B到直线B1D1的距离不变,故△BEF的面积为定值.
又点A到平面BEF的距离为
,故VA-BEF为定值.故正确.
故答案为:(1)(2)(4).
∵B1D1∥平面ABCD,又E、F在直线D1B1上运动,∴EF∥平面ABCD.故(2)正确;
∵对角面与侧面所成角为45°,∴面AEF与面BEF不可能垂直,故(3)不正确;
(4)中由于点B到直线B1D1的距离不变,故△BEF的面积为定值.
又点A到平面BEF的距离为
| ||
| 2 |
故答案为:(1)(2)(4).
点评:本题考查直线与平面平行的判定,棱柱、棱锥、棱台的体积,异面直线及其所成的角,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
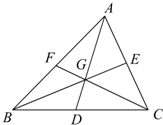 在△ABC中,AD,BE,CF分别是BC,CA,AB边上的中线,G是它们的交点,则下列等式中不正确的是( )
在△ABC中,AD,BE,CF分别是BC,CA,AB边上的中线,G是它们的交点,则下列等式中不正确的是( )A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|