题目内容
求函数y=（sinx+cosx）2+2cos2x的最小正周期= ．
考点：三角函数中的恒等变换应用
专题：三角函数的求值
分析：利用同角三角函数基本关系式、倍角公式、两角和差的正弦公式、三角函数的周期公式即可得出．
解答：
解：y=1+sin 2x+2cos2x=sin 2x+cos 2x+2
=
(
sin2x+
cos2x)+2
=
sin（2x+
）+2．
故最小正周期=
=π．
故答案为：π．
=
| 2 |
| ||
| 2 |
| ||
| 2 |
=
| 2 |
| π |
| 4 |
故最小正周期=
| 2π |
| 2 |
故答案为：π．
点评：本题考查了同角三角函数基本关系式、倍角公式、两角和差的正弦公式、三角函数的周期公式，属于基础题．
练习册系列答案
相关题目
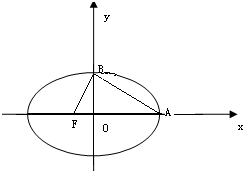已知双曲线的中心在坐标原点，焦点在x轴上，A是右顶点，B是虚轴的上端点，F是左焦点，当BF⊥AB时，此类双曲线称为“黄金双曲线”，其离心率为e=
正方体ABCD-A1B1C1D1的棱长为1，线段B1D1上有两个动点E，F，且EF=函数f（x）的定义域为R，f（2）=4，对?x∈R，f′（x）＞3，则f（x）＞3x-2的解集是（ ）
| A、（-∞，+∞） |
| B、（2，+∞） |
| C、（-∞，2） |
| D、（-2，2） |