题目内容
三条直线两两垂直,现有一条直线与其中两条都成60°,则此直线与另外一条直线所成角为 .
考点:异面直线及其所成的角
专题:空间角
分析:如图所示,OA,OB,OC三条直线两两垂直,OP与两条直线OB,OC都成60°.过点P作PD⊥平面OBC,垂足为点D.可得点D在∠BOC的平分线OM上,连接BD,CD.不妨取OA=OB=OC=2,分别在Rt△OPD中,在△OBD与△OBP中,利用勾股定理和余弦定理,可得
=
.于是∠POD=45°.即可得出∠AOP.
| OD |
| OP |
| ||
| 2 |
解答:
解:如图所示,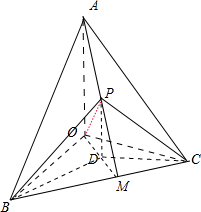
OA,OB,OC三条直线两两垂直,OP与两条直线OB,OC都成60°.
过点P作PD⊥平面OBC,垂足为点D.则点D在∠BOC的平分线OM上,
连接BD,CD.
不妨取OA=OB=OC=2,
在Rt△OPD中,由勾股定理可得PD2=OP2-OD2.
在△OBD与△OBP中,由余弦定理可得:
BD2=OB2+OD2-2OB•OD•cos45°=22+OD2-4OD×
=4+OD2-2
OD,
PB2=OB2+OP2-2OB•OP•cos60°=4+OP2-2OP.
在Rt△BDP中,由勾股定理可得:PB2=BD2+PD2.
∴4+OP2-2OP=4+OD2-2
OD+OP2-OD2,
化为
=
.
∴∠POD=45°.
∴∠AOP=45°.
即直线OP与另外一条直线OA所成角为45°.

OA,OB,OC三条直线两两垂直,OP与两条直线OB,OC都成60°.
过点P作PD⊥平面OBC,垂足为点D.则点D在∠BOC的平分线OM上,
连接BD,CD.
不妨取OA=OB=OC=2,
在Rt△OPD中,由勾股定理可得PD2=OP2-OD2.
在△OBD与△OBP中,由余弦定理可得:
BD2=OB2+OD2-2OB•OD•cos45°=22+OD2-4OD×
| ||
| 2 |
| 2 |
PB2=OB2+OP2-2OB•OP•cos60°=4+OP2-2OP.
在Rt△BDP中,由勾股定理可得:PB2=BD2+PD2.
∴4+OP2-2OP=4+OD2-2
| 2 |
化为
| OD |
| OP |
| ||
| 2 |
∴∠POD=45°.
∴∠AOP=45°.
即直线OP与另外一条直线OA所成角为45°.
点评:本题考查了异面直线所成的角、线面垂直的性质、余弦定理和勾股定理,考查了辅助线的作法,考查了推理能力和计算能力,考查了空间想象能力,属于难题.

练习册系列答案
相关题目
设
=
,
=
,
=
,则
等于( )
| AB |
| a |
| AD |
| b |
| BC |
| c |
| DC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
 正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=
正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=