题目内容
6.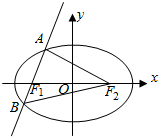 已知F1、F2为椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1(a>b>0)的左、右两个焦点,斜率不为0的直线l过左焦点F1 且交椭圆C于A(x1,y1),B(x2,y2)两点,
已知F1、F2为椭圆C:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1(a>b>0)的左、右两个焦点,斜率不为0的直线l过左焦点F1 且交椭圆C于A(x1,y1),B(x2,y2)两点,(1)求|F1F2|的长度.
(2)求证:S${\;}_{△AB{F}_{2}}$=2|y1-y2|
(3)求△ABF2面积的最大值.
分析 (1)利用椭圆求出a2=6,b2=2,得到c,即可求出|F1F2|.
(2)利用y1•y1<0,求出三角形的面积,然后证明面积为:|y1-y2|.
(3)设直线l的方程为:x=my-2,联立$\left\{{\begin{array}{l}{x=my-2}\\{\frac{x^2}{6}+\frac{y^2}{2}+1}\end{array}}\right.$消去x,利用韦达定理,求出三角形的面积S${\;}_{△AB{F}_{2}}$的表达式利用基本不等式求出最大值.
解答 解:(1)因为a2=6,b2=2
所以$c=\sqrt{{a^2}-{b^2}}=2$…(1分)
故|F1F2|=4…(2分)
(2)证明:因为直线l过F1,
且斜率不为0,所以y1•y1<0…(3分)
所以,${S_{△AB{F_2}}}={S_{△A{F_1}{F_2}}}+{S_{△B{F_1}{F_2}}}=\frac{1}{2}|{{F_1}{F_2}}|•|{y_1}|+\frac{1}{2}|{{F_1}{F_2}}|•|{y_2}|$
=2|y1|+2|y2|=2|y1-y2|…(6分)
(3)由(1)得,F1(-2,0),设直线l的方程为:x=my-2
由$\left\{{\begin{array}{l}{x=my-2}\\{\frac{x^2}{6}+\frac{y^2}{2}+1}\end{array}}\right.$得:(m2+3)y2-4my-2=0
所以,${y_1}+{y_2}=\frac{4m}{{{m^2}+3}},{y_1}•{y_2}=-\frac{2}{{{m^2}+3}}$…(8分)
因此,S${\;}_{△AB{F}_{2}}$=2|y1-y2|=$\sqrt{{{({y_1}+{y_2})}^2}-4{y_1}•{y_2}}$=$2\sqrt{\frac{{16{m^2}}}{{{{({m^2}+3)}^2}}}+\frac{8}{{{m^2}+3}}}$…(8分)
=$\frac{{4\sqrt{6}•\sqrt{{m^2}+1}}}{{{m^2}+3}}=\frac{{4\sqrt{6}}}{{\sqrt{{m^2}+1}+\frac{2}{{\sqrt{{m^2}+1}}}}}$$≤\frac{{4\sqrt{6}}}{{2\sqrt{2}}}=2\sqrt{3}$
…(9分)…(11分)
当且仅当$\sqrt{{m^2}+1}=\frac{2}{{\sqrt{{m^2}+1}}}$,即m=±1时取“=”号
所以,S${\;}_{△AB{F}_{2}}$的最大值为$2\sqrt{3}$…(12分)
点评 本题考查直线与椭圆的位置关系的综合应用,三角形的面积的求法,距离公式的应用,椭圆的简单性质的应用,考查分析问题解决问题的能力.

 名校课堂系列答案
名校课堂系列答案
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | (0,4) | B. | (-4,0) | C. | $(0,\frac{15}{4})$ | D. | $(\frac{1}{2},2)$ |
| A. | 1024 | B. | 1023 | C. | 512 | D. | 511 |
 如图,在多面体ABCDE中,AB⊥平面ACD,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.
如图,在多面体ABCDE中,AB⊥平面ACD,DE∥AB,AC=AD=CD=DE=2,F为CD的中点.