题目内容
1．角α的终边上一点P的坐标为（4a，-3a）（a≠0），求2sinα+cosα的值．分析 由角α终边上一点P的坐标，利用任意角的三角函数定义求出sinα，cosα即可求解结果
解答 解：∵角α终边上一点P（4a，-3a），
∴r=|5a|．
当a＜0时，sinα＞0，cosα＜0，
∴sinα=$\frac{3}{5}$，cosα=-$\frac{4}{5}$，
∴2sinα+cosα=$\frac{2}{5}$；
当a＞0时，sinα＜0，cosα＞0，
sinα=-$\frac{3}{5}$，cosα=$\frac{4}{5}$，
∴2sinα+cosα=-$\frac{2}{5}$．
综上：2sinα+cosα=±$\frac{2}{5}$．
点评 此题考查三角函数的定义，基本知识的考查，注意分类讨论思想的应用．
练习册系列答案
桃李文化快乐暑假武汉出版社系列答案
优秀生快乐假期每一天全新寒假作业本系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
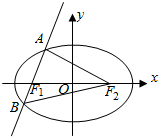已知F1、F2为椭圆C：$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1（a＞b＞0）的左、右两个焦点，斜率不为0的直线l过左焦点F1 且交椭圆C于A（x1，y1），B（x2，y2）两点，
如图，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，∠BAC=90°AB=AC=2，AA1=3．