题目内容
15．已知函数f（x）=$\left\{{\begin{array}{l}{{x^2}-4x+1，x＞0}\\{-1+{{log}_2}（-x），x＜0}\end{array}}$，若函数g（x）=f（x）-a有三个不同的零点x1，x2，x3，则x1+x2+x3的取值范围是（ ）| A． | （0，4） | B． | （-4，0） | C． | $（0，\frac{15}{4}）$ | D． | $（\frac{1}{2}，2）$ |
分析 作函数f（x）=$\left\{{\begin{array}{l}{{x^2}-4x+1，x＞0}\\{-1+{{log}_2}（-x），x＜0}\end{array}}$与y=a的图象，若x1＜x2＜x3，可得x2+x3=4，-3＜-1+log2（-x1）＜1，从而解得．
解答 解：作函数f（x）=$\left\{{\begin{array}{l}{{x^2}-4x+1，x＞0}\\{-1+{{log}_2}（-x），x＜0}\end{array}}$与y=a的图象如下，
不妨设其三个交点的横坐标满足x1＜x2＜x3，
易知x2+x3=4，-3＜-1+log2（-x1）＜1，
解得，$\frac{1}{4}$＜-x1＜4，
故-4＜x1＜-$\frac{1}{4}$，
故0＜x1+x2+x3＜-$\frac{1}{4}$+4=$\frac{15}{4}$，
故选C．
点评 本题考查了分段函数的应用及数形结合的思想应用．
练习册系列答案
名校课堂系列答案
相关题目
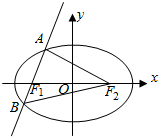已知F1、F2为椭圆C：$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{2}$=1（a＞b＞0）的左、右两个焦点，斜率不为0的直线l过左焦点F1 且交椭圆C于A（x1，y1），B（x2，y2）两点，
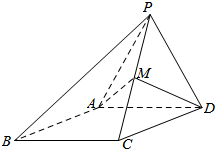如图，四棱锥P-ABCD，侧面PAD是边长为2的正三角形，且与底面ABCD垂直，底面ABCD是∠ABC=60°的菱形，M为PC的中点．
如图，在三棱柱ABC-A1B1C1中，AA1⊥平面ABC，∠BAC=90°AB=AC=2，AA1=3．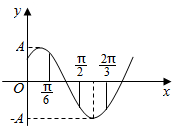
函数f（x）=Asin（ωx+φ）（A，ω，φ是常数，A＞0，ω＞0）的图象如图所示，若$f（{\frac{π}{2}}）=f（{\frac{2π}{3}}）=-f（{\frac{π}{6}}）$，则ω=2．
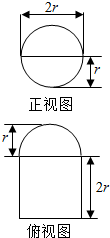圆柱被一个平面截去一部分与半球（半径为r）组成一个几何体，该几何体三视图中的正视图和俯视图如图所示．若半球的半径r=2，则该几何体的表面积为16+20π．