题目内容
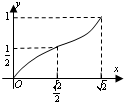
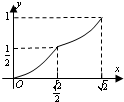
若点P在曲线y=-x2+x+2上移动,且P点横坐标取值范围是[0,
],经过点P的切线的倾斜角为α,则α的取值范围是( )
| 1 |
| 2 |
A、[0,
| ||||
B、[0,
| ||||
C、[
| ||||
D、[
|
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:求导函数,根据切点P的横坐标的取值范围,确定切线斜率的取值范围,从而可得切线的倾斜角的取值范围.
解答:
解:求导函数可得,y′=-2x+1
∵切点P的横坐标的取值范围是[0,
],
∴-2x+1∈[0,1]
设切线的倾斜角为α,则tanα∈[0,1]
∵α∈[0,π)
∴α∈[0,
].
故选:B.
∵切点P的横坐标的取值范围是[0,
| 1 |
| 2 |
∴-2x+1∈[0,1]
设切线的倾斜角为α,则tanα∈[0,1]
∵α∈[0,π)
∴α∈[0,
| π |
| 4 |
故选:B.
点评:本题考查导数知识的运用,考查导数的几何意义,考查直线的倾斜角与斜率,属于基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
设振幅、相位、初相为方程y=Asin(ωx+φ)+b(A>0)的基本量,则方程y=3sin(2x-1)+4的基本量之和为( )
| A、4 | B、2x+3 |
| C、8 | D、2x+1 |
 给出10个数:1,2,4,7,11…46,其规律是:第一个数是1,第二个数比第一个数大1,第三个数比第二个数大2,…以此类推,要计算这10个数的和,现已给出了该问题的程序如图所示,那么框图中判断框①处和执行框②处应分别填入( )
给出10个数:1,2,4,7,11…46,其规律是:第一个数是1,第二个数比第一个数大1,第三个数比第二个数大2,…以此类推,要计算这10个数的和,现已给出了该问题的程序如图所示,那么框图中判断框①处和执行框②处应分别填入( )| A、i≤10?,p=p+i-1 |
| B、i≤9?,p=p+i |
| C、i≤10?,p=p+i |
| D、i≤11?,p=p+i |
有4个兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
在△ABC中,c=18,b=12,C=60°,则cosB=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
在复平面内,满足条件z•(1+i)=2的复数z对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知函数f(x)=cos(2x+φ)的图象沿x轴向左平移
个单位后,得到函数g(x)的图象,则“φ=-
”是“g(x)为偶函数”的( )
| π |
| 12 |
| π |
| 6 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
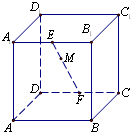 如图:正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱A1B1,CD的中点,点M是EF的动点,FM=x,过点M、直线AB的平面将正方体分成上下两部分,记下面那部分的体积为V(x),则函数V(x)的大致图象是( )
如图:正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱A1B1,CD的中点,点M是EF的动点,FM=x,过点M、直线AB的平面将正方体分成上下两部分,记下面那部分的体积为V(x),则函数V(x)的大致图象是( )