题目内容
19.已知$\overrightarrow{p}$=(a,b),$\overrightarrow{q}$=(c,d),规定向量$\overrightarrow{p}$,$\overrightarrow{q}$之间的一个运算符号“*”,$\overrightarrow{p}$*$\overrightarrow{q}$=(ac-bd,ad+bc),若$\overrightarrow{p}$=(0,1),$\overrightarrow{p}$*$\overrightarrow{q}$=(-4,-3),则$\overrightarrow{q}$等于( )| A. | (3,-4) | B. | (3,4) | C. | (-3,4) | D. | (-3,-4) |
分析 可设$\overrightarrow{q}=(x,y)$,根据运算“*”的定义,便可求得$\overrightarrow{p}*\overrightarrow{q}=(-y,x)=(-4,-3)$,这样即可求出x,y,从而得出$\overrightarrow{q}$的坐标.
解答 解:设$\overrightarrow{q}=(x,y)$,则$\overrightarrow{p}*\overrightarrow{q}=(0-y,0+x)=(-y,x)$=(-4,-3);
∴$\left\{\begin{array}{l}{-y=-4}\\{x=-3}\end{array}\right.$;
∴$\overrightarrow{q}=(-3,4)$.
故选:C.
点评 考查向量坐标的概念,以及根据运算“*”的定义会进行向量坐标的“*”运算.

练习册系列答案
相关题目
4.在四边形ABCD中,若$\overrightarrow{AB}$=(6,1),$\overrightarrow{BC}$=(3,-4),$\overrightarrow{CD}$=(-2,-3),则四边形ABCD的面积是( )
| A. | 20 | B. | 30 | C. | 40 | D. | 50 |
11.已知f(x)=2sinωx(cosωx+sinωx)的图象在x∈[0,1]上恰有一个对称轴和一个对称中心,则实数ω的取值范围为( )
| A. | ($\frac{3π}{8}$,$\frac{5π}{8}$) | B. | [$\frac{3π}{8}$,$\frac{5π}{8}$) | C. | ($\frac{3π}{8}$,$\frac{5π}{8}$] | D. | [$\frac{3π}{8}$,$\frac{5π}{8}$] |
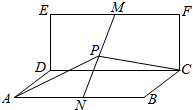 如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=2$\sqrt{2}$,DE=2,AB=4,点M,N分别为线段EF,AB上的动点,点P为MN的中点,则PA+PC的最小值为2$\sqrt{7}$.
如图,矩形CDEF所在的平面与矩形ABCD所在的平面垂直,AD=2$\sqrt{2}$,DE=2,AB=4,点M,N分别为线段EF,AB上的动点,点P为MN的中点,则PA+PC的最小值为2$\sqrt{7}$.