题目内容
已知复数z=
(i是虚数单位),则复数z在复平面内对应的点位于( )
| i2 |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点:复数代数形式的乘除运算,复数的代数表示法及其几何意义
专题:数系的扩充和复数
分析:利用两个复数代数形式的乘除法法则化简复数为z=-
+
i,由此可得它对应点所在的象限.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵复数z=
=
=
=-
+
i,故它对应点在第二象限,
故选:B.
| i2 |
| 1+i |
| -1×(1-i) |
| (1+i)(1-i) |
| -1+i |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故选:B.
点评:本题主要考查复数代数形式的混合运算,复数与复平面内对应点之间的关系,属于基础题.

练习册系列答案
相关题目
设y=ln(2x+3),则y′=( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知集合A={x丨丨x-1丨<2},B={x丨y=lg(x2+x)},设U=R,则A∩(∁UB)等于( )
| A、[3,+∞) |
| B、(-1,0] |
| C、(3,+∞) |
| D、[-1,0] |
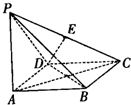 四棱锥P-ABCD的底面为棱形,且∠DAB=60°,PA⊥底面ABCD,AB=2a,PA=2
四棱锥P-ABCD的底面为棱形,且∠DAB=60°,PA⊥底面ABCD,AB=2a,PA=2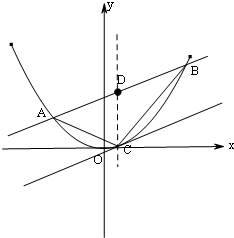 如图,直线l:y=kx+b与抛物线x2=2py(常数p>0)相交于不同的两点A(x1,y1)、B(x2,y2),且|x2-x1|=h(h为定值),线段AB的中点为D,与直线l:y=kx+b平行的切线的切点为C(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).
如图,直线l:y=kx+b与抛物线x2=2py(常数p>0)相交于不同的两点A(x1,y1)、B(x2,y2),且|x2-x1|=h(h为定值),线段AB的中点为D,与直线l:y=kx+b平行的切线的切点为C(不与抛物线对称轴平行或重合且与抛物线只有一个公共点的直线称为抛物线的切线,这个公共点为切点).