题目内容
若f(sinx)=cos19x,则f(cosx)= .
考点:三角函数的化简求值
专题:计算题,三角函数的求值
分析:利用f(cosx)=f[sin(
-x)],将sin(
-x)代入f(sinx)=cos19x,从而得到答案.
| π |
| 2 |
| π |
| 2 |
解答:
解:f(cosx)
=f[sin(
-x)]
=cos[19(
-x)]
=cos(π+
-19x)
=sin19x;
故答案为:-sin19x.
=f[sin(
| π |
| 2 |
=cos[19(
| π |
| 2 |
=cos(π+
| π |
| 2 |
=sin19x;
故答案为:-sin19x.
点评:本题考查了三角函数问题,考查了求解析式问题,属于基本知识的考查.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案
相关题目
函数函数f(x)=cos(sinx)的最小正周期是( )
A、
| ||
| B、π | ||
| C、2m | ||
| D、4m |
在14与
之间插入n个数组成等比数列,若各项总和为
,则此数列的项数( )
| 7 |
| 8 |
| 77 |
| 8 |
| A、4 | B、5 | C、6 | D、7 |
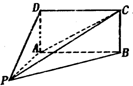 如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.