题目内容

8．设点P是曲线y=x3-$\sqrt{3}$x+$\frac{2}{3}$上的任意一点，在P点处切线倾斜角a的取值范围．

分析 求出函数的导数，由二次函数的性质可得切线斜率范围，结合正切函数图象即可得到所求倾斜角的范围．

解答 解：因y′=3x2-$\sqrt{3}$≥-$\sqrt{3}$，
故切线斜率k=tana≥-$\sqrt{3}$，
则切线倾斜角a的取值范围是[0，$\frac{π}{2}$）∪[$\frac{2π}{3}$，π）．

点评 本题考查导数的运用：求切线的斜率和倾斜角的范围，考查运算能力，属于基础题．

练习册系列答案
相关题目
18．（1）已知集合A={x|3＜x＜7}，B={x|2＜x＜10}，求A∪B，A∩B，∁RA
（2）计算下列各式
①$2{log_5}25+{10^{lg\sqrt{3}}}+ln{e^{（{1-\sqrt{3}}）}}+{（{\sqrt{2}-1}）^0}$
②（2a${\;}^{\frac{2}{3}}$b${\;}^{\frac{1}{2}}$）（-6a${\;}^{\frac{1}{2}}$b${\;}^{\frac{1}{3}}$）÷（-3a${\;}^{\frac{1}{6}}$b${\;}^{\frac{5}{6}}$）
19．全集U={1，2，3，4，5}，集合A={1，2}，集合B={1，3，5}，则图中阴影部分所表示的集合是（　　）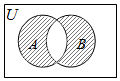
A．{1}B．{1，2，3，5}C．{ 2，3，5}D．{4}
16．（文）已知函数f（x）=sin2ωx+$\sqrt{3}$sinωxcosωx（ω＞0）的最小正周期为π．
（Ⅰ）求ω的值；
（Ⅱ）求函数f（x）在区间[0，$\frac{2π}{3}$]上的取值范围．
3．数列{an}的通项公式为an=3n-23，当Sn取到最小时，n=（　　）
A．5B．6C．7D．8
13．已知集合M={x|x-2＞0，x∈R}，N={y|y=$\sqrt{{x}^{2}+1}$，x∈R}，则M∩N=（　　）
A．{x|x≥1}B．{x|1≤x＜2}C．{x|x＞2}D．{x|x＞2或x＜0}
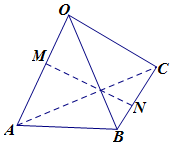20．已知直线l1：ax+by+1=0，（a，b不同时为0），l2：（a-2）x+y+a=0，若b=0且l1⊥l2，求实数a的值．
17．如图，已知三棱锥O-ABC，OA=4，OB=5，OC=3，∠AOB=∠BOC=60°，∠COA=90°，M，N分别是OA，BC的中点，设$\overrightarrow{OA}$=a，$\overrightarrow{OB}$=b，$\overrightarrow{OC}$=c．
（Ⅰ）用a，b，c表示$\overrightarrow{MN}$和$\overrightarrow{AC}$；
（Ⅱ）求直线MN与直线AC所成的角的余弦值．
18．双曲线$\frac{x^2}{9}-{y^2}=1$的实轴长为6．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网