题目内容
已知在△ABC中,角A、B、C的对边分别为a、b、c,已知c=2,向量
=(c,
b),
=(cosC,sinB),且
∥
.
(1)求角C的大小;
(2)若sin(A+B),sin2A,sin(B-A)成等差数列,求边a的大小.
| m |
| 3 |
| n |
| m |
| n |
(1)求角C的大小;
(2)若sin(A+B),sin2A,sin(B-A)成等差数列,求边a的大小.
考点:正弦定理,平面向量数量积的运算
专题:解三角形
分析:(1)利用数量积运算、正弦定理即可得出;
(2)由sin(A+B),sin2A,sin(B-A)成等差数列,可得2sin2A=sin(A+B)+sin(B-A),cosA=0或2sinA=sinB,即2a=b.再利用直角三角形的边角关系、余弦定理即可得出.
(2)由sin(A+B),sin2A,sin(B-A)成等差数列,可得2sin2A=sin(A+B)+sin(B-A),cosA=0或2sinA=sinB,即2a=b.再利用直角三角形的边角关系、余弦定理即可得出.
解答:
解:(1)∵
∥
,
∴
bcosC-csinB=0,
由正弦定理可得:
sinBcosC-sinCsinB=0,
∵sinB≠0,
∴tanC=
,C∈(0,π),
∴C=
.
(2)∵sin(A+B),sin2A,sin(B-A)成等差数列,
∴2sin2A=sin(A+B)+sin(B-A),
化为4sinAcosA=2sinBcosA,
∴cosA=0或2sinA=sinB,即2a=b.
当cosA=0时,A∈(0,π),
∴A=
,
∴a=
=
=
.
当2a=b时.由余弦定理可得:c2=a2+b2-2abcosC,
∴4=a2+4a2-4a2cos
,
化为a2=
,
解得a=
.
| m |
| n |
∴
| 3 |
由正弦定理可得:
| 3 |
∵sinB≠0,
∴tanC=
| 3 |
∴C=
| π |
| 3 |
(2)∵sin(A+B),sin2A,sin(B-A)成等差数列,
∴2sin2A=sin(A+B)+sin(B-A),
化为4sinAcosA=2sinBcosA,
∴cosA=0或2sinA=sinB,即2a=b.
当cosA=0时,A∈(0,π),
∴A=
| π |
| 2 |
∴a=
| c |
| sinC |
| 2 | ||
sin
|
4
| ||
| 3 |
当2a=b时.由余弦定理可得:c2=a2+b2-2abcosC,
∴4=a2+4a2-4a2cos
| π |
| 3 |
化为a2=
| 4 |
| 3 |
解得a=
2
| ||
| 3 |
点评:本题考查了两角和差的正弦公式、正弦定理余弦定理、三角形内角和定理、数量积运算性质、直角三角形的边角关系、分类讨论方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
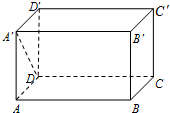 如图,在长方体ABCD-A′B′C′D′中,AB=6,AA′=BC=4,则A′D与BC所成的角等于( )
如图,在长方体ABCD-A′B′C′D′中,AB=6,AA′=BC=4,则A′D与BC所成的角等于( )| A、30° | B、45° |
| C、60° | D、90° |
 一个圆柱形容器里装有水,放在水平面上,现将容器倾斜,这时水面是一个椭圆,当圆柱的母线AB与地面所成角
一个圆柱形容器里装有水,放在水平面上,现将容器倾斜,这时水面是一个椭圆,当圆柱的母线AB与地面所成角