题目内容
7．已知偶函数f（x）的定义域是R，且f（x）在（0，+∞）是增函数，则a=f（-2），b=f（π），c=f（-3）的大小关系是（ ）| A． | a＜c＜b | B． | b＜a＜c | C． | b＜c＜a | D． | c＜a＜b |
分析 利用f（x）是定义在R上的偶函数，化简a，c，利用函数在（0，+∞）上是增函数，可得a，b，c的大小关系．
解答 解：偶函数f（x）的定义域是R，
a=f（-2）=f（2），
b=f（π），
c=f（-3）=f（3），
∵f（x）在（0，+∞）上是增函数，π＞3＞2
∴a＜c＜b
故选：A
点评 本题考查抽象函数及其应用，函数单调性与奇偶性的结合，考查学生分析解决问题的能力，难度中档．
练习册系列答案
阅读快车系列答案
相关题目
15．将角α的终边顺时针旋转$\frac{π}{2}$，则它与以原点为圆心，1为半径的单位圆的交点的坐标是（ ）
| A． | （cosα，sinα） | B． | （cosα，-sinα） | C． | （sinα，-cosα） | D． | （sinα，cosα） |
2．
一个简单几何体的正视图、侧视图如图所示，则其俯视图不可能为：
①长方形；
②正方形；
③圆．
其中正确的是（ ）
一个简单几何体的正视图、侧视图如图所示，则其俯视图不可能为：①长方形；
②正方形；
③圆．
其中正确的是（ ）
| A． | ①② | B． | ②③ | C． | ①③ | D． | ①② |
12．定义区域[x1，x2]的长度为x2-x1（x2＞x1），函数$f（x）=\frac{{（{a^2}+a）x-1}}{{{a^2}x}}（a∈R，a≠0）$的定义域与值域都是[m，n]（n＞m），则区间[m，n]取最大长度时实数a的值为（ ）
| A． | $\frac{{2\sqrt{3}}}{3}$ | B． | -3 | C． | 1 | D． | 3 |
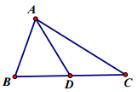已知△ABC中，点D为BC中点，AB=2，AC=4．