题目内容
15.将角α的终边顺时针旋转$\frac{π}{2}$,则它与以原点为圆心,1为半径的单位圆的交点的坐标是( )| A. | (cosα,sinα) | B. | (cosα,-sinα) | C. | (sinα,-cosα) | D. | (sinα,cosα) |
分析 由题意,设坐标为(x,y),则x=cos((α-$\frac{π}{2}$)=sinα,y=sin(α-$\frac{π}{2}$)=-cosα,即可得出结论.
解答 解:由题意,设坐标为(x,y),则x=cos((α-$\frac{π}{2}$)=sinα,y=sin(α-$\frac{π}{2}$)=-cosα,
故选C.
点评 本题考查三角函数的定义,考查诱导公式的运用,比较基础.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
6.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>0}\\{f(x+6),x≤0}\end{array}\right.$,则f(-8)的值是( )
| A. | -2 | B. | 2 | C. | 0 | D. | 1 |
3.若a>b>1,$θ∈(0,\frac{π}{2})$,则( )
| A. | asinθ<bsinθ | B. | absinθ<basinθ | ||
| C. | alogbsinθ<blogasinθ | D. | logasinθ<logbsinθ |
10.设a=sin$\frac{13π}{5}$,$b=cos(-\frac{2π}{5})$,c=tan$\frac{7π}{5}$,则( )
| A. | b<a<c | B. | b<c<a | C. | a<b<c | D. | a<c<b |
7.已知偶函数f(x)的定义域是R,且f(x)在(0,+∞)是增函数,则a=f(-2),b=f(π),c=f(-3)的大小关系是( )
| A. | a<c<b | B. | b<a<c | C. | b<c<a | D. | c<a<b |
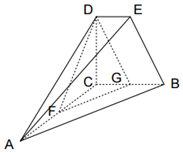 如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.
如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.