题目内容
16.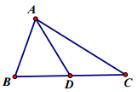 已知△ABC中,点D为BC中点,AB=2,AC=4.
已知△ABC中,点D为BC中点,AB=2,AC=4.(1)若B=$\frac{π}{3}$,求sinA;
(2)若AD=$\sqrt{3}$,求BC.
分析 (1)若B=$\frac{π}{3}$,求出sinC,cosC,即可求sinA;
(2)若AD=$\sqrt{3}$,利用余弦定理建立方程,即可求BC
解答 解:(1)由正弦定理,可得sinC=$\frac{ABsinB}{AC}$=$\frac{\sqrt{3}}{4}$,
∵0<C<π,
∴cosC=$\frac{\sqrt{13}}{4}$,
∴sinA=sin(B+C)=$\frac{\sqrt{3}}{2}×\frac{\sqrt{13}}{4}+\frac{1}{2}×\frac{\sqrt{3}}{4}$=$\frac{\sqrt{39}+\sqrt{3}}{8}$;
(2)设BC=2x,在△ABD中,由余弦定理可得cos∠ADB=$\frac{{x}^{2}-1}{2\sqrt{3}x}$,
△ACD中,由余弦定理可得cos∠ADC=$\frac{{x}^{2}-13}{2\sqrt{3}x}$,
∴$\frac{{x}^{2}-13}{2\sqrt{3}x}$=-$\frac{{x}^{2}-1}{2\sqrt{3}x}$,
∴x=$\sqrt{7}$,
∴BC=2$\sqrt{7}$.
点评 本题考查正弦、余弦定理的运用,考查方程思想,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
6.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>0}\\{f(x+6),x≤0}\end{array}\right.$,则f(-8)的值是( )
| A. | -2 | B. | 2 | C. | 0 | D. | 1 |
7.已知偶函数f(x)的定义域是R,且f(x)在(0,+∞)是增函数,则a=f(-2),b=f(π),c=f(-3)的大小关系是( )
| A. | a<c<b | B. | b<a<c | C. | b<c<a | D. | c<a<b |
4.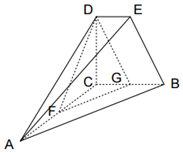 如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.
如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.
(1)求证:平面DFG∥平面ABE;
(2)若AC=2BC=2CD=4,求二面角E-AB-C的正切值.
 如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.
如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.(1)求证:平面DFG∥平面ABE;
(2)若AC=2BC=2CD=4,求二面角E-AB-C的正切值.
6.指数函数y=ax(a>0,a≠1)的反函数图象过点(9,2),则a=( )
| A. | 3 | B. | 2 | C. | 9 | D. | 4 |
 如图,某农户计划在自家后院,背靠院墙用篱笆围出一块约8m2的矩形空地用来养鸡,所需篱笆总长度最小为8m.
如图,某农户计划在自家后院,背靠院墙用篱笆围出一块约8m2的矩形空地用来养鸡,所需篱笆总长度最小为8m.