题目内容
12.定义区域[x1,x2]的长度为x2-x1(x2>x1),函数$f(x)=\frac{{({a^2}+a)x-1}}{{{a^2}x}}(a∈R,a≠0)$的定义域与值域都是[m,n](n>m),则区间[m,n]取最大长度时实数a的值为( )| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | -3 | C. | 1 | D. | 3 |
分析 将函数f(x)化简,首先考虑f(x)的单调性,由题意可得f(m)=n,f(n)=m.,故m,n是方程f(x)的同号的相异实数根.利用韦达定理和判别式,求出m,n的关系.在求最大值
解答 解:解:函数$f(x)=\frac{{({a^2}+a)x-1}}{{{a^2}x}}(a∈R,a≠0)$的定义域是{x|x≠0},则[m,n]是其定义域的子集,
∴[m,n]⊆(-∞,0)或(0,+∞).
化简得f(x)=$\frac{{a}^{2}x+ax-1}{{a}^{2}x}=\frac{1+a}{a}-\frac{1}{{a}^{2}x}$在区间[m,n]上是单调递增,则有$\left\{\begin{array}{l}{f(n)=m}\\{f(m)=n}\end{array}\right.$,
故m,n是方程f(x)=$\frac{1+a}{a}-\frac{1}{{a}^{2}x}$=x的同号相异的实数根,即m,n是方程(ax)2-(a2+a)x+1=0同号相异的实数根.
那么mn=$\frac{1}{{a}^{2}}$,m+n=$\frac{1+a}{a}$,
只需要△>0,即(a2+a)2-4a2>0,
解得:a>1或a<-3.
那么:n-m=$\sqrt{(n+m)^{2}-4mn}$=$\sqrt{-3(\frac{1}{a}-\frac{1}{3})^{2}+\frac{4}{3}}$,
故n-m的最大值为$\frac{2\sqrt{3}}{3}$,此时解得:a=3.
故选:D.
点评 本题考查了函数性质的方程的运用,有一点综合性,利用函数关系,构造新的函数解题.属于中档题,分类讨论思想的运用,增加了本题的难度,解题时注意.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.$\frac{{tan{{18}°}+tan{{42}°}+tan{{120}°}}}{{tan{{198}°}tan{{222}°}}}$=( )
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
3.若a>b>1,$θ∈(0,\frac{π}{2})$,则( )
| A. | asinθ<bsinθ | B. | absinθ<basinθ | ||
| C. | alogbsinθ<blogasinθ | D. | logasinθ<logbsinθ |
7.已知偶函数f(x)的定义域是R,且f(x)在(0,+∞)是增函数,则a=f(-2),b=f(π),c=f(-3)的大小关系是( )
| A. | a<c<b | B. | b<a<c | C. | b<c<a | D. | c<a<b |
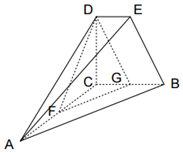 如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.
如图,DE∥BC,BC=2DE,CA⊥CB,CA⊥CD,CB⊥CD,F、G分别是AC、BC中点.