题目内容
设函数f(θ)=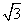 sin θ+cos θ,其中,角θ的顶
sin θ+cos θ,其中,角θ的顶 点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x
点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x ,y),且0≤θ≤π.
,y),且0≤θ≤π.
(1)若点P的坐标为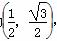 ,求f(θ)的值;
,求f(θ)的值;
(2)若点P(x,y)为平面区域Ω: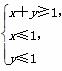 上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
上的一个动点,试确定角θ的取值范围,并求函数f(θ)的最小值和最大值.
解析: (1)由点P的坐标和三角函数的定义可得 于是f(θ)=
于是f(θ)=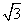 si
si n θ+cos θ=
n θ+cos θ=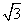 ×
× +
+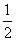 =2.
=2.
(2)作出平面区域Ω( 即三角形区域ABC)如图所示,其中A(1,0),B(1,1),C(0,1).于是0≤θ≤
即三角形区域ABC)如图所示,其中A(1,0),B(1,1),C(0,1).于是0≤θ≤ .
.

又f(θ)=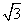 sin θ+cos θ=2sin
sin θ+cos θ=2sin ,且
,且 ≤θ+
≤θ+ ≤
≤ ,故当θ+
,故当θ+ =
= ,即θ=
,即θ= 时,f(θ)取得最大值,且最大值等于2;当θ+
时,f(θ)取得最大值,且最大值等于2;当θ+ =
= ,即θ=0时,f(θ)取得最小值,且最小值等于1.
,即θ=0时,f(θ)取得最小值,且最小值等于1.

练习册系列答案
相关题目
 中,
中, ,
,
 是
是 的重心,
的重心, 是
是 的最大值为_________
的最大值为_________
 >y-a,⑤
>y-a,⑤ >
>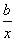 这五个式子中,恒成立的所有不等式的序号是________.
这五个式子中,恒成立的所有不等式的序号是________.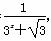 ,先分别求f(0)+f(1),f(-1)+f(2),f(-2)+f(3),然后归纳猜想一般性结论,并给出证明.
,先分别求f(0)+f(1),f(-1)+f(2),f(-2)+f(3),然后归纳猜想一般性结论,并给出证明. B.
B. C.
C. D.
D.
 ,且下列四个关系:
,且下列四个关系: ; ②
; ②  ; ③
; ③  ; ④
; ④  .
. 的个数是 .
的个数是 .