题目内容
设f(x)＝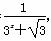
，先分别求f(0)＋f(1)，f(－1)＋f(2)，f(－2)＋f(3)，然后归纳猜想一般性结论，并给出证明．
解析：f(0)＋f(1)＝
同理可得：f(－1)＋f(2)＝
，
f(－2)＋f(3)＝，并注意到在这三个特殊式子中，自变量之和均等于1.
归纳猜想得：当x1＋x2＝1时，均有f(x1)＋f(x2)＝.
证明：设x1＋x2＝1，
f(x1)＋f(x2)
练习册系列答案
相关题目
题目内容
设f(x)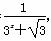＝，先分别求f(0)＋f(1)，f(－1)＋f(2)，f(－2)＋f(3)，然后归纳猜想一般性结论，并给出证明．
解析：f(0)＋f(1)＝同理可得：f(－1)＋f(2)＝，
f(－2)＋f(3)＝，并注意到在这三个特殊式子中，自变量之和均等于1.
归纳猜想得：当x1＋x2＝1时，均有f(x1)＋f(x2)＝.
证明：设x1＋x2＝1，
f(x1)＋f(x2)
，则
的值为（ ）
B、
C、
D、
≤0的解集为________．
n(n＋1) C．n2－1 D.
63＋73＋83＝________________(结果用具体数字作答)．
且z＝5y－x的最大值为a，最小值为b，则a－b的值是( )
sin θ＋cos θ，其中，角θ的顶
点与坐标原点重合，始边与x轴非负半轴重合，终边经过点P(x
，y)，且0≤θ≤π.
，求f(θ)的值；
上的一个动点，试确定角θ的取值范围，并求函数f(θ)的最小值和最大值．
，则下列结论正确的是（ ）
是偶函数 （B）
上是增函数 
－
＝1的焦点，PQ是过焦点F1的弦，那么|PF2|＋|QF2|－
|PQ|的值是__________．