Question

3．某市地产数据研究的数据显示，2016年该市新建住宅销售均价走势如下图所示，3月至7月房价上涨过快，政府从8月采取宏观调控措施，10月份开始房价得到很好的抑制．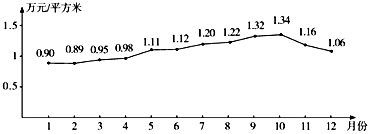

（Ⅰ）地产数据研究所发现，3月至7月的各月均价y（万元/平方米）与月份x之间具有较强的线性相关关系，试求y关于x的回归方程；
（Ⅱ）政府若不调控，依此相关关系预测第12月份该市新建住宅的销售均价．
（从3月到7月的参考数据：$\sum_{i=1}^{5}$x_i=25，$\sum_{i=1}^{5}$y_i=5.36，$\sum_{i=1}^{5}$（x_i-$\overline{x}$）（y_i-$\overline{y}$）=0.64；回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中斜率和截距的最小二乘法估计公式分别为：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．）

Answer 1

分析 （Ⅰ）由题意，计算$\overline{x}$，$\overline{y}$，求出回归系数$\widehat{b}$，$\widehat{a}$，即可写出回归方程；（Ⅱ）利用（Ⅰ）中回归方程，计算x=12时$\widehat{y}$的值即可．

解答 解：（Ⅰ）由题意，得出下表；

月份x	3	4	5	6	7
均价y	0.95	0.98	1.11	1.12	1.20

计算$\overline{x}$=$\frac{1}{5}$×$\sum_{i=1}^{5}$x_i=5，$\overline{y}$=$\frac{1}{5}$×$\sum_{i=1}^{5}$y_i=1.072，$\sum_{i=1}^{5}$（x_i-$\overline{x}$）（y_i-$\overline{y}$）=0.64，
∴$\widehat{b}$=$\frac{\sum_{i=1}^{n}{（x}_{i}-\overline{x}）{（y}_{i}-\overline{y}）}{{\sum_{i=1}^{n}{（x}_{i}-\overline{x}）}^{2}}$=$\frac{0.64}{{（3-5）}^{2}{+（4-5）}^{2}{+（5-5）}^{2}{+（6-5）}^{2}{+（7-5）}^{2}}$=0.064，
$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=1.072-0.064×5=0.752，
∴从3月到6月，y关于x的回归方程为$\widehat{y}$=0.064x+0.752；
（Ⅱ）利用（Ⅰ）中回归方程，计算x=12时，$\widehat{y}$=0.064×12+0.752=1.52；
即可预测第12月份该市新建住宅销售均价为1.52万元/平方米．

点评 本题考查了回归直线方程的求法与应用问题，正确计算是解题的关键．