题目内容
12.抛掷一枚质地均匀的骰子两次,记事件A={两次的点数均为奇数},B={两次的点数之和小于7},则P(B|A)=( )| A. | $\frac{1}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
分析 此是一个条件概率模型的题,可以求出事件A包含的基本事件数,与在A发生的条件下,事件B包含的基本事件数,再用公式求出概率.
解答 解:由题意事件记A={两次的点数均为奇数},包含的基本事件数是(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5)共9个基本事件,在A发生的条件下,B={两次的点数之和小于7},包含的基本事件数是(1,1),(1,3),(1,5),(3,1),(3,3 ),(5,1)共6个基本事件.∴P(B|A)=$\frac{6}{9}=\frac{2}{3}$
故选:D.
点评 本题考查条件概率,考查古典概型概率的计算,解题的关键是正确理解与运用条件概率公式.属于基础题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
4.已知某海滨浴场的海浪高度(单位:米)是时间(单位:小时,0≤t≤24)的函数,记作y=f(t),如表是某日各时的浪高数据:
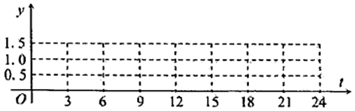
(Ⅰ)在如图的网格中描出所给的点;
(Ⅱ)观察图,从y=at+b,y=at2+bt+c,y=Acos(ωx+p)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(Ⅲ)依据规定,当海浪高度高于1.25米时蔡对冲浪爱好者开放,请依据(Ⅱ)的结论判断一天内的8:00到20:00之间有多长时间可供冲浪爱好者进行活动.

| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 |
(Ⅱ)观察图,从y=at+b,y=at2+bt+c,y=Acos(ωx+p)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(Ⅲ)依据规定,当海浪高度高于1.25米时蔡对冲浪爱好者开放,请依据(Ⅱ)的结论判断一天内的8:00到20:00之间有多长时间可供冲浪爱好者进行活动.
1.在△ABC中,内角A,B,C所对应的边分别为a,b,c,且a=3b,4bsinC=c,则sinA等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{9}$ | D. | $\frac{3}{16}$ |
2.对于函数y=f(x),部分x与y的对应关系如表:
数列{xn}满足x1=2,且对任意n?N﹡,点(xn,xn+1)都在函数y=f(x)的图象上,则x1+x2+x3+…+x2017的值为( )
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 7 | 4 | 5 | 8 | 1 | 3 | 5 | 2 | 6 |
| A. | 9400 | B. | 9408 | C. | 9410 | D. | 9414 |
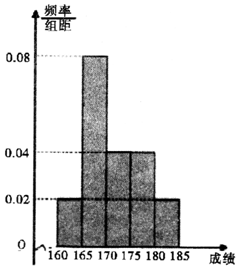 近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如图所示:
近期中央电视台播出的《中国诗词大会》火遍全国.某选拔赛后,随机抽取100名选手的成绩,按成绩由低到高依次分为第1,2,3,4,5组,制成频率分布直方图如图所示: