题目内容
13.已知圆C的半径为2,圆心在x轴的正半轴上,直线3x+4y+4=0与圆C相切,则圆C的一般方程是x2+y2-4x=0;.分析 根据圆心在x轴的正半轴上,设出圆心坐标,由直线3x+4y+4=0与圆C相切,可得圆心到直线的距离等于半径,可得圆C的一般方程.
解答 解:由题意,圆C的半径为2,圆心在x轴的正半轴上,设出圆心坐标(a,0),(a>0),直线方程3x+4y+4=0.
则圆心到直线的距离d=$\frac{3a+4}{5}$=2,
解得:a=2.
可得圆的标准方程为:(x-2)2+y2=4;
则圆C的一般方程:x2+y2-4x=0;
故答案为:x2+y2-4x=0.
点评 本题主要考查直线和圆的位置关系的判断,根据直线和圆相切的等价条件是解决本题的关键.

练习册系列答案
相关题目
4.已知某海滨浴场的海浪高度(单位:米)是时间(单位:小时,0≤t≤24)的函数,记作y=f(t),如表是某日各时的浪高数据:
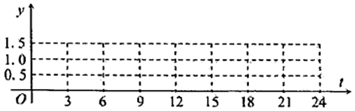
(Ⅰ)在如图的网格中描出所给的点;
(Ⅱ)观察图,从y=at+b,y=at2+bt+c,y=Acos(ωx+p)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(Ⅲ)依据规定,当海浪高度高于1.25米时蔡对冲浪爱好者开放,请依据(Ⅱ)的结论判断一天内的8:00到20:00之间有多长时间可供冲浪爱好者进行活动.

| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 |
(Ⅱ)观察图,从y=at+b,y=at2+bt+c,y=Acos(ωx+p)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(Ⅲ)依据规定,当海浪高度高于1.25米时蔡对冲浪爱好者开放,请依据(Ⅱ)的结论判断一天内的8:00到20:00之间有多长时间可供冲浪爱好者进行活动.
1.在△ABC中,内角A,B,C所对应的边分别为a,b,c,且a=3b,4bsinC=c,则sinA等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{9}$ | D. | $\frac{3}{16}$ |
8.某公司为对本公司的160名员工的身体状况进行调查,先将员工随机编号为1,2,3,…,159,160,采用系统抽样的方法(等间距地抽取,每段抽取一个个体)将抽取的一个样本.已知抽取的员工中最小的两个编号为5,21,那么抽取的员工中,最大的编号应该是( )
| A. | 141 | B. | 142 | C. | 149 | D. | 150 |
2.对于函数y=f(x),部分x与y的对应关系如表:
数列{xn}满足x1=2,且对任意n?N﹡,点(xn,xn+1)都在函数y=f(x)的图象上,则x1+x2+x3+…+x2017的值为( )
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| y | 7 | 4 | 5 | 8 | 1 | 3 | 5 | 2 | 6 |
| A. | 9400 | B. | 9408 | C. | 9410 | D. | 9414 |