题目内容
 在三棱锥P-ABC中,△ABC为正三角形,∠PCA=90°,D为PA中点,二面角P-AC-B的大小为为120°,PC=2,AB=2
在三棱锥P-ABC中,△ABC为正三角形,∠PCA=90°,D为PA中点,二面角P-AC-B的大小为为120°,PC=2,AB=2| 3 |
(1)求证:AC⊥BD;
(2)求BD与底面ABC所成的角,
(3)求三棱锥P-ABC的体积.
考点:直线与平面所成的角,棱柱、棱锥、棱台的体积
专题:综合题,空间位置关系与距离
分析:(1)欲证AC⊥BD,可证AC垂直于BD所在的平面,故取AC的中点E,并连接DE、BE,则问题得证.
(2)需确定∠DBE为BD与平面ABC所成角、∠BED为二面角P-AC-B的平面角,则在△BDE中两次利用余弦定理问题解决.
(3)求出P到平面ABC的距离,利用锥体的体积公式,即可求三棱锥P-ABC的体积.
(2)需确定∠DBE为BD与平面ABC所成角、∠BED为二面角P-AC-B的平面角,则在△BDE中两次利用余弦定理问题解决.
(3)求出P到平面ABC的距离,利用锥体的体积公式,即可求三棱锥P-ABC的体积.
解答:
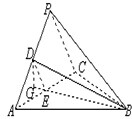 (1)证明:取AC的中点E,并连接DE、BE,如图所示,
(1)证明:取AC的中点E,并连接DE、BE,如图所示,
因为D是PA中点,E是AC的中点,所以DE∥PC,
又∠PCA=90°,即PC⊥AC,所以DE⊥AC,
且正三角形ABC中,BE⊥AC,
所以AC⊥平面BDE,又BD?平面BDE,
所以AC⊥BD.
(2)解:在平面BDE中作EF⊥BE,交BD于F,且EF⊥AC,BE∩AC=E,
所以EF⊥平面ABC,则∠FBE即∠DBE为BD与平面ABC所成角,
其中DE=2×
=1,BE=2
sin60°=3,
由AC⊥平面BDE知,∠BED为二面角P-AC-B的平面角,即∠BED=120°,
由余弦定理得,BD2=1+9-2×1×3cos120°=13,即BD=
,
所以cos∠DBE=
=
,
所以∠DBE=arccos
.
即BD与平面ABC所成角为arccos
.
(3)解:因为D为PA的中点,所以P到平面ABC的距离h=2DG=
,
所以VP-ABC=
S△ABCh=
×
×(2
)2×
=3.
 (1)证明:取AC的中点E,并连接DE、BE,如图所示,
(1)证明:取AC的中点E,并连接DE、BE,如图所示,因为D是PA中点,E是AC的中点,所以DE∥PC,
又∠PCA=90°,即PC⊥AC,所以DE⊥AC,
且正三角形ABC中,BE⊥AC,
所以AC⊥平面BDE,又BD?平面BDE,
所以AC⊥BD.
(2)解:在平面BDE中作EF⊥BE,交BD于F,且EF⊥AC,BE∩AC=E,
所以EF⊥平面ABC,则∠FBE即∠DBE为BD与平面ABC所成角,
其中DE=2×
| 1 |
| 2 |
| 3 |
由AC⊥平面BDE知,∠BED为二面角P-AC-B的平面角,即∠BED=120°,
由余弦定理得,BD2=1+9-2×1×3cos120°=13,即BD=
| 13 |
所以cos∠DBE=
| 9+13-1 | ||
2×3×
|
7
| ||
| 26 |
所以∠DBE=arccos
7
| ||
| 26 |
即BD与平面ABC所成角为arccos
7
| ||
| 26 |
(3)解:因为D为PA的中点,所以P到平面ABC的距离h=2DG=
| 3 |
所以VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| 3 |
| 3 |
点评:本题考查线线垂直的判定、二面角的平面角及线面夹角的定义,同时考查余弦定理与空间想象能力,考查锥体体积的计算.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
等比数列前三项分别为x,2x+2,3x+3,则第四项为( )
A、-
| ||
B、
| ||
| C、4x+4 | ||
| D、(2x+2)÷[(3x+3)x] |
 省少年篮球队要从甲、乙两所体校选拔队员.现将这两所体校共20名学生的身高绘制成如茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”.
省少年篮球队要从甲、乙两所体校选拔队员.现将这两所体校共20名学生的身高绘制成如茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”.