题目内容
 如图,三棱锥A-BCD各棱长都为1,且M、N分别是AB、CD的中点,
如图,三棱锥A-BCD各棱长都为1,且M、N分别是AB、CD的中点,(1)求MN和BD所成角;
(2)求该三棱锥体积与它的内切球体积之比.
考点:棱柱、棱锥、棱台的体积,球的体积和表面积,异面直线及其所成的角
专题:综合题,空间位置关系与距离
分析:(1)取BC中点O,连接MO,NO,则∠MNO(或其补角)为MN和BD所成角;
(2)求出三棱锥的高,可得三棱锥的体积,求出内切球的半径,可得内切球的体积,即可求出三棱锥体积与它的内切球体积之比.
(2)求出三棱锥的高,可得三棱锥的体积,求出内切球的半径,可得内切球的体积,即可求出三棱锥体积与它的内切球体积之比.
解答:
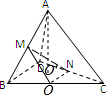 解:(1)取BC中点O,连接MO,NO,则
解:(1)取BC中点O,连接MO,NO,则
∵N是CD的中点,
∴ON∥BD,
∴∠MNO(或其补角)为MN和BD所成角.
∵MO=NO,MO⊥NO,
∴∠MNO=45°,即MN和BD所成角为45°;
(2)作AO′⊥平面ABC,则AO′=
=
,
∴三棱锥体积为
×
×
=
.
设内切球的半径为r,则4×
×
r=
.
∴r=
,
∴内切球体积为
π×(
)3=
π,
∴三棱锥体积与它的内切球体积之比为
.
 解:(1)取BC中点O,连接MO,NO,则
解:(1)取BC中点O,连接MO,NO,则∵N是CD的中点,
∴ON∥BD,
∴∠MNO(或其补角)为MN和BD所成角.
∵MO=NO,MO⊥NO,
∴∠MNO=45°,即MN和BD所成角为45°;
(2)作AO′⊥平面ABC,则AO′=
1-(
|
| ||
| 3 |
∴三棱锥体积为
| 1 |
| 3 |
| ||
| 4 |
| ||
| 3 |
| ||
| 12 |
设内切球的半径为r,则4×
| 1 |
| 3 |
| ||
| 4 |
| ||
| 12 |
∴r=
| ||
| 12 |
∴内切球体积为
| 4 |
| 3 |
| ||
| 12 |
| ||
| 216 |
∴三棱锥体积与它的内切球体积之比为
6
| ||
| π |
点评:本题考查线线角,考查锥体体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 在四棱锥P-ABCD中,四边形ABCD正方形,PA⊥平面ABCD,且PA=AB=2,E为PD的中点.
在四棱锥P-ABCD中,四边形ABCD正方形,PA⊥平面ABCD,且PA=AB=2,E为PD的中点.
 省少年篮球队要从甲、乙两所体校选拔队员.现将这两所体校共20名学生的身高绘制成如茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”.
省少年篮球队要从甲、乙两所体校选拔队员.现将这两所体校共20名学生的身高绘制成如茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”. 如图,在多面体ABCDEFG中,四边形ABCD是边长为2的正方形,平面ABG,平面ADF,平面CDE都与平面ABCD垂直,且△ABG、△ADF、△CDE都是正三角形.
如图,在多面体ABCDEFG中,四边形ABCD是边长为2的正方形,平面ABG,平面ADF,平面CDE都与平面ABCD垂直,且△ABG、△ADF、△CDE都是正三角形. 已知,如图,AB是圆O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.
已知,如图,AB是圆O的直径,AC切⊙O于点A,AC=AB,CO交⊙O于点P,CO的延长线交⊙O于点F,BP的延长线交AC于点E.