题目内容
11.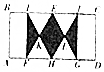 如图所示,已知长方形ABCD中,BC=2AB,△EFG与△HIJ均为等边三角形,F、H、G在AD上,I、E、J在BC上,连接FI,GJ,且AB∥FI∥GJ,若AF=GD,则向长方形ABCD内投掷一个点,该点落在阴影区域内的概率为$\frac{\sqrt{3}}{6}$.
如图所示,已知长方形ABCD中,BC=2AB,△EFG与△HIJ均为等边三角形,F、H、G在AD上,I、E、J在BC上,连接FI,GJ,且AB∥FI∥GJ,若AF=GD,则向长方形ABCD内投掷一个点,该点落在阴影区域内的概率为$\frac{\sqrt{3}}{6}$.
分析 根据几何概型的概率计算公式,设BC=2AB=2,AF=GD=x,
根据勾股定理求出x的值,由对称性求出阴影面积,计算所求的概率值.
解答 解:长方形ABCD中,设BC=2AB=2,AF=GD=x,
∴FG=2-2x,
由勾股定理得(1-x)2+12=(2-2x)2,
解得x=1-$\frac{\sqrt{3}}{3}$,
∴FG=$\frac{2\sqrt{3}}{3}$;
由对称性知,
S阴影=$\frac{1}{2}$S矩形FGJI=$\frac{1}{2}$FG•IF=$\frac{1}{2}$×$\frac{2\sqrt{3}}{3}$×1=$\frac{\sqrt{3}}{3}$;
∴该点落在阴影区域内的概率为
P=$\frac{{S}_{阴影}}{{S}_{长方形ABCD}}$=$\frac{\frac{\sqrt{3}}{3}}{2×1}$=$\frac{\sqrt{3}}{6}$.
故答案为:$\frac{\sqrt{3}}{6}$.
点评 本题考查了几何概型的概率计算问题,解题的关键是计算阴影部分的面积,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.在数列{an}中,a1=2,an+1=an+lg(1+$\frac{1}{n}$),则an的值为( )
| A. | 2+lgn | B. | 2+(n-1)lgn | C. | 2+nlgn | D. | 1+nlgn |
6.若方程$2sin(2x+\frac{π}{6})=m$在$x∈[0,\frac{π}{2}]$上有两个不相等的实数解x1,x2,则x1+x2=( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
16.三棱锥A-BCD内接于半径为2的球O,BC过球心O,当三棱锥A-BCD体积取得最大值时,三棱锥A-BCD的表面积为( )
| A. | $6+4\sqrt{3}$ | B. | $8+2\sqrt{3}$ | C. | $4+6\sqrt{3}$ | D. | $8+4\sqrt{3}$ |
15.命题“若x=3,则x2-9x+18=0”的逆命题、否命题和逆否命题中,假命题的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |