题目内容

2．写出下列不等式的解集
（1）tanx-1≤0．
（2）-1≤tanx＜$\sqrt{3}$．

分析 （1）根据正切函数的图象与性质解不等式即可；
（2）根据正切函数的图象与性质求出不等式的解集．

解答 解：（1）tanx-1≤0，
∴tanx≤1，
解得-$\frac{π}{2}$+kπ＜x≤$\frac{π}{4}$+kπ，k∈Z，
∴不等式的解集是{x|-$\frac{π}{2}$+kπ＜x≤$\frac{π}{4}$+kπ，k∈Z}；
（2）-1≤tanx＜$\sqrt{3}$，
解得-$\frac{π}{4}$+kπ≤x＜$\frac{π}{3}$+kπ，k∈Z，
∴不等式的解集是{x|-$\frac{π}{4}$+kπ≤x＜$\frac{π}{3}$+kπ，k∈Z}．

点评 本题考查了利用正切函数的图象与性质解不等式的应用问题，是基础题．

练习册系列答案
相关题目
12．已知矩形ABCD的周长为18，把它沿图中的虚线折成正四棱柱，则这个正四棱柱的外接球表面积的最小值为36π．
13．已知α，β是两个不同的平面，m，n是两条不同的直线，则下列五个命题：
①如果m⊥α，n∥β，α∥β，那么m⊥n；
②如果m∥α，n∥β，m⊥n，那么α∥β；
③如果m⊥α，n⊥β，m⊥n，那么α⊥β；
④如果m⊥α，n∥β，m⊥n，那么α∥β；
⑤如果m∥α，m∥β，α∩β=n，那么m∥n．
其中正确的命题有①③⑤．（填写所有正确命题的编号）
10．设函数f（x）=x2-alnx，g（x）=（a-2）x
（Ⅰ）求函数f（x）的单调区间；
（Ⅱ）若函数F（x）=f（x）-g（x）有两个零点x1，x2
（1）求满足条件的最小正整数a的值；
（2）求证：F′（$\frac{{x}_{1}+{x}_{2}}{2}$）＞0．
17．已知tanx=3，tany=2，则tan（x-y）的值是$\frac{1}{7}$．
7．设F1、F2分别是离心率为$\frac{\sqrt{2}}{2}$的椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左、右焦点，经过点F2且与x轴垂直的直线l被椭圆截得的弦长为$\sqrt{2}$．
（Ⅰ）求椭圆C的方程；
（Ⅱ）设A，B是C上的两个动点，线段AB的中垂线与C交于P、Q两点，线段AB的中点M在直线l上，求$\overrightarrow{{F}_{1}P}•\overrightarrow{{F}_{1}Q}$的取值范围．
14．已知点P（$\sqrt{3}$，1），Q（cosx，sinx），O为坐标原点，函数f（x）=$\overrightarrow{OP}$•$\overrightarrow{QP}$．
（1）求函数f（x）的最小值及此时x的值；
（2）若A为△ABC的内角，f（A）=4，BC=3，△ABC的面积为$\frac{3\sqrt{3}}{4}$，求△ABC的周长．
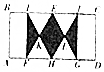11．如图所示，已知长方形ABCD中，BC=2AB，△EFG与△HIJ均为等边三角形，F、H、G在AD上，I、E、J在BC上，连接FI，GJ，且AB∥FI∥GJ，若AF=GD，则向长方形ABCD内投掷一个点，该点落在阴影区域内的概率为$\frac{\sqrt{3}}{6}$．
6．已知cosα-sinα=$\frac{5\sqrt{2}}{13}$，α∈（0，$\frac{π}{4}$）．
（1）求sinαcosα的值；
（2）求$\frac{cos2α}{cos（\frac{π}{4}+α）}$的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网