题目内容
某政府准备建造一个椭圆游泳池(a>b),椭圆的一个焦点到椭圆上的点的最大距离是最小距离的4倍.
(1)求此游泳池所在椭圆的离心率;
(2)已知椭圆的焦距为120米,在椭圆的长轴上的M1、M2处设计两个喷水头,使分出的水花形成有相等半径的圆M1,圆M2,且圆M1与圆M2外切,同时喷出的水不能落到椭圆形游泳池之外,试求两圆的最大半径.
(1)求此游泳池所在椭圆的离心率;
(2)已知椭圆的焦距为120米,在椭圆的长轴上的M1、M2处设计两个喷水头,使分出的水花形成有相等半径的圆M1,圆M2,且圆M1与圆M2外切,同时喷出的水不能落到椭圆形游泳池之外,试求两圆的最大半径.
考点:圆方程的综合应用
专题:应用题,圆锥曲线的定义、性质与方程
分析:(1)根据椭圆的一个焦点到椭圆上的点的最大距离是最小距离的4倍,可以得到a,c的关系,即可求此游泳池所在椭圆的离心率;
(2)以⊙M1与⊙M2的切点为原点,M1、M2所在的线为x轴建立平面直角坐标系.依题意可知圆的方程,设出圆M2的方程,联立消去y,根据位置与椭圆相切可知判别式等于0求得r,
(2)以⊙M1与⊙M2的切点为原点,M1、M2所在的线为x轴建立平面直角坐标系.依题意可知圆的方程,设出圆M2的方程,联立消去y,根据位置与椭圆相切可知判别式等于0求得r,
解答:
解:(1)最大距离为a+c,最小距离为a-c
∴a+c=4(a-c),
∴3a=5c,
∴e=
(2)由题知:c=12百米∴a=20百米 b=16百米
∴椭圆方程为
+
=1
以⊙M1与⊙M2切点为原点,以M1、M2所在直线为X轴建立平面直角坐标系
设⊙M2方程为(x-r)2+y2=r2
联立得
,
∴9x2-100xr+6400=0
∵⊙M2内切与椭圆内
∴△=(-100r)2-4×9×6400=0,
∴r=4.8百米
∴点M1在长轴中点左4.8百米处,点M2在长轴中点右4.8百米处,且⊙M1、⊙M2半径均为4.8百米
∴a+c=4(a-c),
∴3a=5c,
∴e=
| 3 |
| 5 |
(2)由题知:c=12百米∴a=20百米 b=16百米
∴椭圆方程为
| x2 |
| 400 |
| y2 |
| 256 |
以⊙M1与⊙M2切点为原点,以M1、M2所在直线为X轴建立平面直角坐标系
设⊙M2方程为(x-r)2+y2=r2
联立得
|
∴9x2-100xr+6400=0
∵⊙M2内切与椭圆内
∴△=(-100r)2-4×9×6400=0,
∴r=4.8百米
∴点M1在长轴中点左4.8百米处,点M2在长轴中点右4.8百米处,且⊙M1、⊙M2半径均为4.8百米
点评:本题主要考查了椭圆的应用,考查椭圆的性质,考查了学生数形结合的思想和解决实际问题的能力,属于中档题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
函数f(x)=
sin(ωx+φ)(x∈R,ω>0,|φ|<
)的部分图象如图所示,则ω,φ的值分别是( )
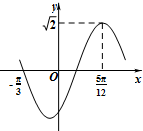
| 2 |
| π |
| 2 |

A、2,-
| ||
B、2,-
| ||
C、4,-
| ||
D、4,
|
直线l经过坐标原点和点(-1,-1),则直线l的倾斜角是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
 设椭圆Γ1的中心和抛物线Γ2的顶点均为原点O,Γ1、Γ2的焦点均在x轴上,过Γ2的焦点F作直线l,与Γ2交于A、B两点,在Γ1、Γ2上各取两个点,将其坐标记录于下表中:
设椭圆Γ1的中心和抛物线Γ2的顶点均为原点O,Γ1、Γ2的焦点均在x轴上,过Γ2的焦点F作直线l,与Γ2交于A、B两点,在Γ1、Γ2上各取两个点,将其坐标记录于下表中: