题目内容
已知函数f(x)=lnx+
+ax,x∈(0,+∞)(a为实常数).若f(x)在[2,+∞)上是单调函数,则a的取值范围是( )
| 1 |
| x |
A、(-∞,-
| ||
B、(-∞,-
| ||
C、(-∞,0)∪[
| ||
D、(-∞,0)∪(
|
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:求出函数的导数,通过a与0的大小比较,判断导函数的符号,研究函数的单调性,求出a 的范围.
解答:
解:f′(x)=
-
+a=
,
当a≥0时,ax2+x-1在[2,+∞)上恒大于零,即f′(x)>0,符合要求.
当a<0时,令g(x)=ax2+x-1,g(x)在[2,+∞)上只能恒小于零,
故△=1+4a≤0或
解得a≤-
,
∴a的取值范围是(-∞,-
]∪[0,+∞).
故选:B.
| 1 |
| x |
| 1 |
| x2 |
| ax2+x-1 |
| x2 |
当a≥0时,ax2+x-1在[2,+∞)上恒大于零,即f′(x)>0,符合要求.
当a<0时,令g(x)=ax2+x-1,g(x)在[2,+∞)上只能恒小于零,
故△=1+4a≤0或
|
| 1 |
| 4 |
∴a的取值范围是(-∞,-
| 1 |
| 4 |
故选:B.
点评:本题考查函数的导数应用,函数的单调性以及分类讨论思想的应用,考查计算能力.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
已知圆的方程式x2+y2=36,记过点P(1,2)的最长弦和最短弦分别为AB、CD,则直线AB、CD的斜率之和等于( )
| A、-1 | ||
B、
| ||
| C、1 | ||
D、-
|
若用m,n表示两条不同的直线,用α表示一个平面,则下列命题正确的是( )
| A、若m∥n,n?α,则m∥α |
| B、若m∥α,n?α,则m∥n |
| C、若m⊥n,n?α,则m⊥α |
| D、若m⊥α,n?α,则m⊥n |
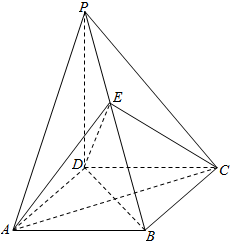 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是菱形,∠BAD=60°,AB=2,PD=