题目内容
8.已知P(2,0),Q是圆$\left\{{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}}\right.$上一动点,求PQ的中点轨迹方程,并说明轨迹是什么样的曲线.分析 根据题意,设PQ的中点为M,其坐标为(x,y),由P、Q的坐标计算可得$\left\{\begin{array}{l}{x=\frac{2+cosθ}{2}}\\{y=\frac{sinθ}{2}}\end{array}\right.$,将其变形为普通方程可得(x-1)2+y2=$\frac{1}{4}$,由圆的标准方程分析可得答案.
解答 解:根据题意,设PQ的中点为M,其坐标为(x,y),
又由P(2,0),Q是圆$\left\{{\begin{array}{l}{x=cosθ}\\{y=sinθ}\end{array}}\right.$上一动点,
则有$\left\{\begin{array}{l}{x=\frac{2+cosθ}{2}}\\{y=\frac{sinθ}{2}}\end{array}\right.$,
变形可得(x-1)2+y2=$\frac{1}{4}$,
则其轨迹为以(1,0)为圆心,半径为$\frac{1}{2}$的圆.
点评 本题考查参数方程的应用,关键是求出PQ中点的参数方程.

练习册系列答案
相关题目
3.函数$f(x)={(\frac{1}{2})^x}$与g(x)=-|x|在区间(-∞,0)上的单调性为( )
| A. | 都是增函数 | B. | f(x)为减函数,g(x)为增函数 | ||
| C. | 都是减函数 | D. | f(x)为增函数,g(x)为减函数 |
13.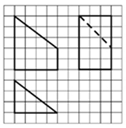 如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )
如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )
 如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )
如图网络纸上小正方形的边长为1,粗实(虚)线画出的是某几何体的三视图,则该几何图的体积为( )| A. | 12 | B. | 18 | C. | 20 | D. | 24 |
17.某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,在学习积极性高的25名学生中有7名不太主动参加班级工作,而在积极参加班级工作的24名学生中有6名学生学习积极性一般.
(1)填写下面列联表;
(2)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(3)试运用独立性检验的思想方法分析:能否在犯错误概率不超过0.001的前提下认为学生的学习积极性与对待班级工作的态度有关系.
(观测值表如下)
(1)填写下面列联表;
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | |||
| 学习积极性一般 | |||
| 合计 |
(3)试运用独立性检验的思想方法分析:能否在犯错误概率不超过0.001的前提下认为学生的学习积极性与对待班级工作的态度有关系.
(观测值表如下)
| P(K2≥k0) | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 5.024 | 6.635 | 7.879 | 10.828 |