题目内容
将函数f（x）=sinx向左平移
个单位，得到函数y=g（x）的图象，则函数y=g（x）是（ ）
| π |
| 2 |
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数又是偶函数 |
| D、非奇非偶函数 |
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由函数图象的平移法则，“左加右减，上加下减”，我们可得函数f（x）的图象向右平移a个单位得到函数f（x-a）的图象，再根据原函数的解析式为y=sinx，向左平移量为
个单位，易得平移后的图象对应的函数解析式．再根据函数解析式即可判断其奇偶性．
| π |
| 2 |
解答：
解：根据函数图象的平移变换的法则：函数f（x）的图象向右平移a个单位得到函数f（x-a）的图象，
故函数y=sinx的图象向左平移
个单位后得到的图象对应的函数解析式是y=sin（x+
），
由诱导公式得y=cosx，由于cos（-x）=cosx，故y=sin（x+
）为偶函数偶函数，其图象关于y轴对称．
故答案为：B．
故函数y=sinx的图象向左平移
| π |
| 2 |
| π |
| 2 |
由诱导公式得y=cosx，由于cos（-x）=cosx，故y=sin（x+
| π |
| 2 |
故答案为：B．
点评：本题考查的知识点函数y=Asin（ωx+φ）的图象变换，其中熟练掌握函数图象的平移法则，“左加右减，上加下减”，是解答本题的关键．本题还考查函数奇偶性的判定，属于中档题．
练习册系列答案
相关题目
若α∈（0，
），且sin2α+cos2α=
，则tanα的值等于（ ）
| π |
| 2 |
| 3 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设sinα=
（
＜α＜π），tan（π-β）=
，则tan（α-2β）=（ ）
| 3 |
| 5 |
| π |
| 2 |
| 1 |
| 2 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
已知非零向量
⊥
，则下列各式正确的是（ ）
| a |
| b |
A、|
| ||||||||
B、|
| ||||||||
C、|
| ||||||||
D、|
|
设U=R，A={x|x＞0}，B={x|x＞1}，则A∪B=（ ）
| A、{x|0≤x＜1} |
| B、{x|0＜x≤1} |
| C、{x|x＞0} |
| D、{x|x＞1} |
若函数f（x）=3ax2+6x-1，若f（x）≤0在R上恒成立，则a的取值范围是（ ）
| A、（-∞，-3） | ||
B、(-∞，-
| ||
| C、（-∞，-3] | ||
D、(-∞，-
|
i是虚数单位，若复数z=
，则复数z的实部与虚部的和是（ ）
| 3+i |
| 1-i |
| A、3 | B、1+2i |
| C、2 | D、1-2i |
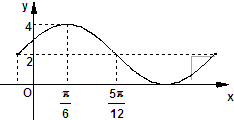已知函数f（x）=Asin（ωx+ϕ）+B的一部分图象如图所示，如果A＞0，ω＞0，|φ|＜