题目内容
11.求函数y=sinx+$\sqrt{3}$cosx的周期,对称轴方程并指出图象可由正弦曲线经过怎样的变化得到.分析 利用辅助角公式先化简函数,结合三角函数的图象和性质进行求解即可.
解答 解:y=sinx+$\sqrt{3}$cosx=2($\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx)=2sin(x+$\frac{π}{3}$),
则函数的周期T=2π,
由x+$\frac{π}{3}$=kπ+$\frac{π}{2}$,即x=kπ+$\frac{π}{6}$,k∈Z,即函数的对称轴为x=kπ+$\frac{π}{6}$,k∈Z.
函数y=sinx的图象上的点向左平移$\frac{π}{3}$个单位得到y=sin(x+$\frac{π}{3}$)的图象,
然后横坐标不变,纵坐标变为原来的2倍得到y=2sin(x+$\frac{π}{3}$).
点评 本题主要考查三角函数的图象变换以及三角函数的性质,根据三角函数的周期变换和平移变换法则是解决本题的关键.

练习册系列答案
相关题目
1.集合A={x|y=lg(-x2+2x)},B={x||x|≤1},则A∩B=( )
| A. | {x|1≤x≤2} | B. | {x|0<x≤1} | C. | {x|-1≤x≤0} | D. | {x|x≤2} |
2.若$\overrightarrow a=(1,1,k)$,$\overrightarrow b=(2,-1,1)$,$\overrightarrow a$与$\overrightarrow b$的夹角为60°,则k的值为( )
| A. | 0或-2 | B. | 0或2 | C. | -2 | D. | 2 |
16.“$α=\frac{π}{6}$”是“$sinα=\frac{1}{2}$”的( )条件.
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
20.已知集合M={(x,y)|x+y-2≤0,x≥0,y≥0},集合N={$(x,y)|y≤\sqrt{x},y≥0$},若点P∈M,则P∈M∩N的概率为( )
| A. | $\frac{7}{18}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{3}{4}$ |
1.若反比例函数f(x)=$\frac{k}{x}$的图象在第一象限内单调递减,则k的取值范围( )
| A. | k≥0 | B. | k≤0 | C. | k>0 | D. | k<0 |
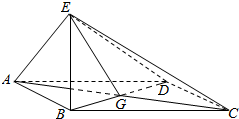 如图四棱锥E-ABCD,底面四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
如图四棱锥E-ABCD,底面四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.