题目内容
1.集合A={x|y=lg(-x2+2x)},B={x||x|≤1},则A∩B=( )| A. | {x|1≤x≤2} | B. | {x|0<x≤1} | C. | {x|-1≤x≤0} | D. | {x|x≤2} |
分析 求出A中x的范围确定出A,求出B中不等式的解集确定出B,即可确定出两集合的交集.
解答 解:由A中y=lg(-x2+2x),得到-x2+2x>0,即x(x-2)<0,
解得:0<x<2,即A={x|0<x<2},
由B中不等式解得:-1≤x≤1,
则A∩B={x|0<x≤1},
故选:B.
点评 此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
相关题目
17.已知正四棱台ABCD-A1B1C1D1中,上底面A1B1C1D1边长为1,下底面ABCD边长为2,侧棱与底面所成的角为60°,则异面直线AD1与B1C所成角的余弦值为$\frac{1}{4}$.
9.已知函数f(x)=x+$\frac{4}{x}$,g(x)=2x+a,若?x1∈[$\frac{1}{2}$,3],?x2∈[2,3],使得f(x1)≥g(x2),则实数a的取值范围是( )
| A. | a≤1 | B. | a≥1 | C. | a≤0 | D. | a≥0 |
16.过y2=2px焦点F的直线交抛物线于A,B,若|BF|=$\frac{6}{5}$,|AF|=$\frac{6}{7}$,则抛物线方程( )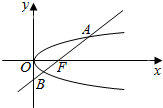

| A. | y2=x | B. | y2=2x | C. | y2=3x | D. | y2=4x |
6.已知全集A={1,2,3,4,5,6},B={y|y=2x-1,x∈A},则A∩B=( )
| A. | {1,2,3,4} | B. | {1,2,3} | C. | {1,3,5} | D. | {2,4,6} |
13.已知集合M={0,1,2},N={y|y=sin$\frac{π}{2}$x,x∈M},则M∩N=( )
| A. | {-1,0,1} | B. | {-1,0} | C. | {0,1} | D. | {0,1,2} |
10.有A、B、C、D、E五位学生的数学成绩x与物理成绩y(单位:分)如下表:
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)若学生F的数学成绩为90分,试根据(1)求出的线性回归方程,预测其物理成绩(保留整数)
(参考数值:80×70+75×66+70×68+65×64+60×62=23190$8{0^2}+7{5^2}+7{0^2}+6{5^2}+6{0^2}=24750,\hat b=\frac{{\sum_{i=1}^5{x_i}{y_i}-n\bar x\bar y}}{{\sum_{i=1}^5x_i^2-n{{\bar x}^2}}},\hat a$=$\overline{y}$$-\hat b$$\overline{x}$.
| x | 80 | 75 | 70 | 65 | 60 |
| y | 70 | 66 | 68 | 64 | 62 |
(2)若学生F的数学成绩为90分,试根据(1)求出的线性回归方程,预测其物理成绩(保留整数)
(参考数值:80×70+75×66+70×68+65×64+60×62=23190$8{0^2}+7{5^2}+7{0^2}+6{5^2}+6{0^2}=24750,\hat b=\frac{{\sum_{i=1}^5{x_i}{y_i}-n\bar x\bar y}}{{\sum_{i=1}^5x_i^2-n{{\bar x}^2}}},\hat a$=$\overline{y}$$-\hat b$$\overline{x}$.