题目内容
6．直线x-y+2$\sqrt{2}$=0上的点P到圆x2+y2=1的切线长最短为$\sqrt{3}$．分析 利用切线和点到圆心的距离关系即可得到结论．
解答 解：圆x2+y2=1的圆心坐标C（0，0），半径R=1．
要使切线长最小，则只需要点P到圆心的距离最小，
此时最小值为圆心C到直线的距离d=$\frac{2\sqrt{2}}{\sqrt{2}}$=2，
此时切线长的最小值为$\sqrt{4-1}$=$\sqrt{3}$，
故答案为：$\sqrt{3}$．
点评 本题考查切线长的最小值的求法，是中档题，解题时要认真审题，注意点到直线的距离公式的合理运用．
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
相关题目
16．过y2=2px焦点F的直线交抛物线于A，B，若|BF|=$\frac{6}{5}$，|AF|=$\frac{6}{7}$，则抛物线方程（ ）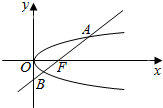
| A． | y2=x | B． | y2=2x | C． | y2=3x | D． | y2=4x |
如图，在三棱锥P-ABC中，D，E，F分别为棱PC，AC，AB的中点．已知PA⊥AC，AB⊥BC，PA=6，AB=BC=8，DF=5．
1．两个数4和9的等比中项是（ ）
| A． | 6 | B． | ±6 | C． | $\frac{13}{2}$ | D． | ±$\frac{13}{2}$ |
18．将函数y=sinx的图象上的点的横坐标扩大为原来的2倍，纵坐标不变得到图象C1，再将图象C1向右平移$\frac{π}{3}$个单位得到的图象C2，则图象C2所对应的函数的解析式为（ ）
| A． | $y=sin（{\frac{1}{2}x-\frac{π}{3}}）$ | B． | $y=sin（{\frac{1}{2}x-\frac{π}{6}}）$ | C． | $y=sin（{2x-\frac{π}{3}}）$ | D． | $y=sin（{2x-\frac{2π}{3}}）$ |
15．命题“?x∈[1，2]，x2-a≤0”为真命题的一个充要条件是（ ）
| A． | a≥4 | B． | a≤4 | C． | a≥5 | D． | a≤5 |