题目内容
16.“$α=\frac{π}{6}$”是“$sinα=\frac{1}{2}$”的( )条件.| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
分析 “$α=\frac{π}{6}$”⇒“$sinα=\frac{1}{2}$”,反之不成立,例如α=$\frac{5π}{6}$.即可判断出结论.
解答 解:“$α=\frac{π}{6}$”⇒“$sinα=\frac{1}{2}$”,反之不成立,例如α=$\frac{5π}{6}$.
因此“$α=\frac{π}{6}$”是“$sinα=\frac{1}{2}$”的充分不必要条件.
故选:A.
点评 本题考查了简易逻辑的判定方法、三角函数求值,考查了推理能力,属于基础题.

练习册系列答案
相关题目
6.已知全集A={1,2,3,4,5,6},B={y|y=2x-1,x∈A},则A∩B=( )
| A. | {1,2,3,4} | B. | {1,2,3} | C. | {1,3,5} | D. | {2,4,6} |
7.在各项均为正数的等比数列{an}中,若a5a6=9,则log3a1+log3a2+…+log3a10=( )
| A. | 12 | B. | 2+log35 | C. | 8 | D. | 10 |
4.已知函数$f(x)=2sin({ωx+\frac{π}{6}})({ω>0})$的图象与x轴交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列,把函数f(x)图象沿x轴向左平移$\frac{π}{6}$个单位,得到函数g(x)的图象.关于函数g(x),下列说法正确的是( )
| A. | 在$[{\frac{π}{4},\frac{π}{2}}]$上是增函数 | |
| B. | 其图象关于直线$x=-\frac{π}{4}$对称 | |
| C. | 函数g(x)是奇函数 | |
| D. | 当$x∈[{\frac{π}{6},\frac{2π}{3}}]$时,函数g(x)的值域是[-2,1] |
1.化简tan20°+4sin20°的结果为( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |
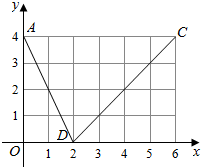 如图,函数f(x)的图象是折线段ABC,其中点A,B,C的坐标分别为(0,4),(2,0),(6,4),则f{f[f(2)]}=( )
如图,函数f(x)的图象是折线段ABC,其中点A,B,C的坐标分别为(0,4),(2,0),(6,4),则f{f[f(2)]}=( )