题目内容
19.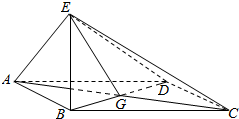 如图四棱锥E-ABCD,底面四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.
如图四棱锥E-ABCD,底面四边形ABCD为菱形,G为AC与BD的交点,BE⊥平面ABCD.(Ⅰ)求证:AC⊥平面BED;
(Ⅱ)若∠ABC=120°,AB=2,AE=2,求AE与平面BED所成角的大小.
分析 (Ⅰ)根据线面垂直的判定定理即可证明:AC⊥平面BED;
(Ⅱ)由(Ⅰ)可知,AE与平面BED所成角为∠AEG,求出AG,即可求AE与平面BED所成角的大小.
解答 (Ⅰ)证明:∵四边形ABCD为菱形,
∴AC⊥BD,
∵BE⊥平面ABCD,
∴AC⊥BE,
∵BD∩BE=B,
∴AC⊥平面BED;
(Ⅱ)解:由(Ⅰ)可知,AE与平面BED所成角为∠AEG.
∵∠ABC=120°,AB=2,
∴AG=$\sqrt{3}$,
∴sin∠AEG=$\frac{\sqrt{3}}{2}$,
∴∠AEG=60°.
点评 本题主要考查线面垂直的判定,以及线面角的计算,要求熟练掌握相应的判定定理.

练习册系列答案
相关题目
9.已知函数f(x)=x+$\frac{4}{x}$,g(x)=2x+a,若?x1∈[$\frac{1}{2}$,3],?x2∈[2,3],使得f(x1)≥g(x2),则实数a的取值范围是( )
| A. | a≤1 | B. | a≥1 | C. | a≤0 | D. | a≥0 |
10.有A、B、C、D、E五位学生的数学成绩x与物理成绩y(单位:分)如下表:
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)若学生F的数学成绩为90分,试根据(1)求出的线性回归方程,预测其物理成绩(保留整数)
(参考数值:80×70+75×66+70×68+65×64+60×62=23190$8{0^2}+7{5^2}+7{0^2}+6{5^2}+6{0^2}=24750,\hat b=\frac{{\sum_{i=1}^5{x_i}{y_i}-n\bar x\bar y}}{{\sum_{i=1}^5x_i^2-n{{\bar x}^2}}},\hat a$=$\overline{y}$$-\hat b$$\overline{x}$.
| x | 80 | 75 | 70 | 65 | 60 |
| y | 70 | 66 | 68 | 64 | 62 |
(2)若学生F的数学成绩为90分,试根据(1)求出的线性回归方程,预测其物理成绩(保留整数)
(参考数值:80×70+75×66+70×68+65×64+60×62=23190$8{0^2}+7{5^2}+7{0^2}+6{5^2}+6{0^2}=24750,\hat b=\frac{{\sum_{i=1}^5{x_i}{y_i}-n\bar x\bar y}}{{\sum_{i=1}^5x_i^2-n{{\bar x}^2}}},\hat a$=$\overline{y}$$-\hat b$$\overline{x}$.
7.在各项均为正数的等比数列{an}中,若a5a6=9,则log3a1+log3a2+…+log3a10=( )
| A. | 12 | B. | 2+log35 | C. | 8 | D. | 10 |
4.已知函数$f(x)=2sin({ωx+\frac{π}{6}})({ω>0})$的图象与x轴交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列,把函数f(x)图象沿x轴向左平移$\frac{π}{6}$个单位,得到函数g(x)的图象.关于函数g(x),下列说法正确的是( )
| A. | 在$[{\frac{π}{4},\frac{π}{2}}]$上是增函数 | |
| B. | 其图象关于直线$x=-\frac{π}{4}$对称 | |
| C. | 函数g(x)是奇函数 | |
| D. | 当$x∈[{\frac{π}{6},\frac{2π}{3}}]$时,函数g(x)的值域是[-2,1] |
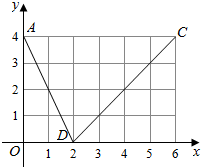 如图,函数f(x)的图象是折线段ABC,其中点A,B,C的坐标分别为(0,4),(2,0),(6,4),则f{f[f(2)]}=( )
如图,函数f(x)的图象是折线段ABC,其中点A,B,C的坐标分别为(0,4),(2,0),(6,4),则f{f[f(2)]}=( )