题目内容
20.已知集合M={(x,y)|x+y-2≤0,x≥0,y≥0},集合N={$(x,y)|y≤\sqrt{x},y≥0$},若点P∈M,则P∈M∩N的概率为( )| A. | $\frac{7}{18}$ | B. | $\frac{1}{2}$ | C. | $\frac{7}{12}$ | D. | $\frac{3}{4}$ |
分析 根据题意,画出图形,根据图形,求出集合M∩N表示的平面区域d的面积S1和集合M表示的区域D的面积S,再利用几何概型求出对应的概率.
解答 解:由集合M={(x,y)|x+y-2≤0,x≥0,y≥0},
集合N={$(x,y)|y≤\sqrt{x},y≥0$},
则集合M∩N={(x,y)|$\left\{\begin{array}{l}{x+y-2≤0}\\{y≤\sqrt{x}}\end{array}\right.$,x≥0,y≥0},
图象如图,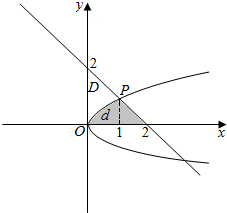
∴集合M∩N中的点所构成的平面区域d的面积为
S1=${∫}_{0}^{1}$$\sqrt{x}$dx+${∫}_{1}^{2}$(2-x)dx=$\frac{2}{3}$•${x}^{\frac{3}{2}}$${|}_{0}^{1}$+(2x-$\frac{1}{2}$x2)${|}_{1}^{2}$
=$\frac{2}{3}$+(2×2-$\frac{1}{2}$×22)-(2×1-$\frac{1}{2}$×12)
=$\frac{7}{6}$,
集合M表示的区域D的面积为S=$\frac{1}{2}$×2×2=2,
所以点P∈M∩N的概率为P=$\frac{{S}_{1}}{S}$=$\frac{\frac{7}{6}}{2}$=$\frac{7}{12}$.
故选:C.
点评 本题考查了几何概型的应用问题,也考查了利用定积分求平面区域的面积问题,是综合性题目.

练习册系列答案
相关题目
10.有A、B、C、D、E五位学生的数学成绩x与物理成绩y(单位:分)如下表:
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)若学生F的数学成绩为90分,试根据(1)求出的线性回归方程,预测其物理成绩(保留整数)
(参考数值:80×70+75×66+70×68+65×64+60×62=23190$8{0^2}+7{5^2}+7{0^2}+6{5^2}+6{0^2}=24750,\hat b=\frac{{\sum_{i=1}^5{x_i}{y_i}-n\bar x\bar y}}{{\sum_{i=1}^5x_i^2-n{{\bar x}^2}}},\hat a$=$\overline{y}$$-\hat b$$\overline{x}$.
| x | 80 | 75 | 70 | 65 | 60 |
| y | 70 | 66 | 68 | 64 | 62 |
(2)若学生F的数学成绩为90分,试根据(1)求出的线性回归方程,预测其物理成绩(保留整数)
(参考数值:80×70+75×66+70×68+65×64+60×62=23190$8{0^2}+7{5^2}+7{0^2}+6{5^2}+6{0^2}=24750,\hat b=\frac{{\sum_{i=1}^5{x_i}{y_i}-n\bar x\bar y}}{{\sum_{i=1}^5x_i^2-n{{\bar x}^2}}},\hat a$=$\overline{y}$$-\hat b$$\overline{x}$.
15.命题“?x∈[1,2],x2-a≤0”为真命题的一个充要条件是( )
| A. | a≥4 | B. | a≤4 | C. | a≥5 | D. | a≤5 |
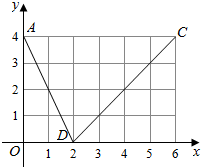 如图,函数f(x)的图象是折线段ABC,其中点A,B,C的坐标分别为(0,4),(2,0),(6,4),则f{f[f(2)]}=( )
如图,函数f(x)的图象是折线段ABC,其中点A,B,C的坐标分别为(0,4),(2,0),(6,4),则f{f[f(2)]}=( )