题目内容
一个半径为1球内切于一个正方体,切点为A,B,C,D,E,F,那么多面体ABCDEF的体积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:由题意知这个正方体的棱长为2,切点为A,B,C,D,E,F构成一个正八面体,沿AD、BE、CF切开这个正八面体,切开该图形后的四面体B-AOF为八面体的
,由此能求出多面体ABCDEF的体积.
| 1 |
| 8 |
解答:
解:∵一个半径为1球内切于一个正方体,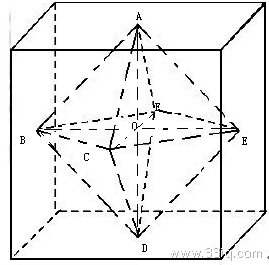
∴这个正方体的棱长为2,
切点为A,B,C,D,E,F构成一个正八面体,如图,
沿AD、BE、CF切开这个正八面体,
设AD、BE、CF交于点O,
则OA=OB=OC=OD=OE=OF=1,
切开该图形后的四面体B-AOF为八面体的
,
∵S△AOF=
×1×1=
,
VB-AOF=
×
×1=
,
∴多面体ABCDEF的体积V=8VB-AOF=8×
=
.
故选:D.

∴这个正方体的棱长为2,
切点为A,B,C,D,E,F构成一个正八面体,如图,
沿AD、BE、CF切开这个正八面体,
设AD、BE、CF交于点O,
则OA=OB=OC=OD=OE=OF=1,
切开该图形后的四面体B-AOF为八面体的
| 1 |
| 8 |
∵S△AOF=
| 1 |
| 2 |
| 1 |
| 2 |
VB-AOF=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
∴多面体ABCDEF的体积V=8VB-AOF=8×
| 1 |
| 6 |
| 4 |
| 3 |
故选:D.
点评:本题考查多面体的求法,是中档题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
设
=(cosα,sinα),
=(cosα,1-
),若
⊥
,则锐角α为( )
| a |
| b |
| 5 |
| 4sinα |
| a |
| b |
| A、15° | B、30° |
| C、45° | D、60° |
类比下列平面内的结论,在空间中仍能成立的是( )
①平行于同一直线的两条直线平行;
②垂直于同一直线的两条直线平行;
③如果一条直线与两条平行线中的一条垂直,则必与另一条垂直;
④如果一条直线与两条平行线中的一条相交,则必与另一条相交.
①平行于同一直线的两条直线平行;
②垂直于同一直线的两条直线平行;
③如果一条直线与两条平行线中的一条垂直,则必与另一条垂直;
④如果一条直线与两条平行线中的一条相交,则必与另一条相交.
| A、①②④ | B、①③ |
| C、②④ | D、①③④ |
设命题p:命题“?x∈R,x2+x+1=0”的否定是“?x∈R,x2+x+1≠0”;命题q:“x>2”是“|x-1|>1”的充分不必要条件,则( )
| A、“p或q”为真 |
| B、“p且q”为真 |
| C、p真q假 |
| D、p,q均为假命题 |
若
、
是夹角为60°的两个单位向量,则向量
=2
+
与向量
=-3
+2
的夹角为( )
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| b |
| e1 |
| e2 |
| A、120° | B、90° |
| C、60° | D、30° |
若双曲线
-
=1的一个焦点到一条渐近线的距离为2a,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2 | ||
B、
| ||
C、
| ||
D、
|
若函数f(x)=(x-1)(x-2)(x-3)(x-4),则f′(2)=( )
| A、-1 | B、0 | C、1 | D、2 |



