题目内容
10.如图,在周长为8的矩形ABCD中,E,F分别为BC,DA的中点.将矩形ABCD沿着线段EF折起,使得∠DFA=60°.设G为AF上一点,且满足CF∥平面BDG.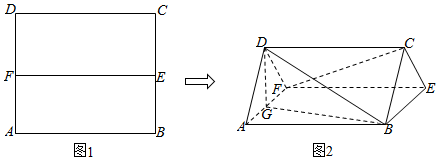
(Ⅰ)求证:EF⊥DG;
(Ⅱ)求证:G为线段AF的中点;
(Ⅲ)求线段CG长度的最小值.
分析 (Ⅰ)由E,F分别为BC,DA的中点,可证EF⊥FD,EF⊥FA,从而EF⊥平面DFA,即可得证EF⊥DG.
(Ⅱ)由AB∥EF∥CD,易证四边形ABCD为平行四边形.连接AC,设AC∩BD=O,则AO=CO,又由CF∥平面BDG,利用线面平行的性质可证CF∥OG,可证OG为中位线,即G为线段AF的中点.
(Ⅲ)由已知可得△DFA为等边三角形,且DG⊥FA,又EF⊥DG,可得DG⊥平面ABEF,设BE的中点为H,连接GH,CH,可得CG2=GH2+CH2,设DF=x,由题意得CG2=(4-2x)2+($\frac{\sqrt{3}}{2}$x)2=$\frac{19}{4}$x2-16x+16,利用二次函数的图象和性质即可得解线段CG长度的最小值.
解答 (本小题满分14分)
(Ⅰ)证明:因为在折起前的矩形ABCD中,E,F分别为BC,DA的中点,
所以EF⊥FD,EF⊥FA,
又因为FD∩FA=F,
所以EF⊥平面DFA.…(2分)
又因为DG?平面DFA,
所以EF⊥DG.…(4分)
(Ⅱ)证明:因为在折起前的矩形ABCD中,E,F分别为BC,DA的中点,
所以在立体图中,AB∥EF∥CD.
即在立体图中,四边形ABCD为平行四边形.
连接AC,设AC∩BD=O,则AO=CO.…(6分)
又因为CF∥平面BDG,CF?平面ACF,平面ACF∩平面BDG=OG,
所以CF∥OG,
所以在△ACF中,OG为中位线,
即G为线段AF的中点.…(9分)
(Ⅲ)解:因为G为线段AF的中点,∠DFA=60°.
所以△DFA为等边三角形,且DG⊥FA,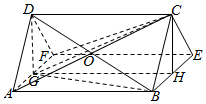
又因为EF⊥DG,EF∩FA=F,
所以DG⊥平面ABEF.
设BE的中点为H,连接GH,CH,
易得四边形DGHC为平行四边形,
所以CH⊥平面ABEF,
所以CG2=GH2+CH2.…(11分)
设DF=x,由题意得CH=DG=$\frac{\sqrt{3}}{2}$x,GH=CD=4-2x,
所以CG2=(4-2x)2+($\frac{\sqrt{3}}{2}$x)2=$\frac{19}{4}$x2-16x+16,…(13分)
所以当x=$\frac{32}{19}$时,CG2min=$\frac{48}{19}$.
所以线段CG长度的最小值为$\frac{4\sqrt{57}}{19}$.…(14分)
点评 本题考查的知识点是直线与平面平行的判定,二次函数的图象和性质的应用,熟练掌握空间直线与平面位置关系的定义、判定定理、性质定理是解答本题的关键,属于中档题.

| A. | $\frac{1}{3}$ | B. | 1 | C. | $\frac{5}{3}$ | D. | 2 |
 如图,四棱锥P-ABCD的底面为平行四边形,M为PC中点.
如图,四棱锥P-ABCD的底面为平行四边形,M为PC中点.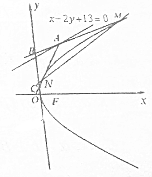 过直线x-2y+13=0上一动点A(A不在y轴上)作抛物线y2=8x的两条切线,M,N为切点,直线AM,AN分别与y轴交于点B,C.
过直线x-2y+13=0上一动点A(A不在y轴上)作抛物线y2=8x的两条切线,M,N为切点,直线AM,AN分别与y轴交于点B,C.