题目内容
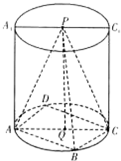 如图,已知圆柱的上、下底面圆心分别为P、Q,AA1与CC1是圆柱的母线,正方形ABCD内接于下底面圆Q,AB=kAA1=2,连接PA、PB、PC.
如图,已知圆柱的上、下底面圆心分别为P、Q,AA1与CC1是圆柱的母线,正方形ABCD内接于下底面圆Q,AB=kAA1=2,连接PA、PB、PC.(Ⅰ)当k=
| 2 |
(Ⅱ)当k为何值时,Q点在平面PBC内的射影恰好是△PBC的重心.
考点:直线与平面所成的角,旋转体(圆柱、圆锥、圆台)
专题:空间位置关系与距离,空间角
分析:(Ⅰ)当k=
时,AA1=
,AB=2,以D为原点,DA为x轴,DC为y轴,建立空间直角坐标系,利用向量法能求出直线PA与平面PBC所成角的正弦值.
(Ⅱ)取BC中点E,连结QE,PE,则QE⊥BC,PE⊥BC,过Q作QF⊥PE,交PE于F,由已知得F是Q点在平面PBC内的射影,利用向量法能求出当k为
时,Q点在平面PBC内的射影恰好是△PBC的重心.
| 2 |
| 2 |
(Ⅱ)取BC中点E,连结QE,PE,则QE⊥BC,PE⊥BC,过Q作QF⊥PE,交PE于F,由已知得F是Q点在平面PBC内的射影,利用向量法能求出当k为
| ||
| 2 |
解答:
解:(Ⅰ)当k=
时,AA1=
,AB=2,
以D为原点,DA为x轴,DC为y轴,建立空间直角坐标系,
P(1,1,
),A(2,0,0),
B(2,2,0),C(0,2,0),
=(1,-1,-
),
=(1,1,-
),
=(-1,1,-
),
设平面PBC的法向量
=(x,y,z),
,
取x=1,得
=(0,
,1),
设直线PA与平面PBC所成角为θ,
sinθ=|cos<
,
>|=|
|=
,
∴直线PA与平面PBC所成角的正弦值为
.
(Ⅱ)取BC中点E,连结QE,PE,则QE⊥BC,PE⊥BC,
∴BC⊥平面PQE,
过Q作QF⊥PE,交PE于F,∵QF?平面PQE,∴BC⊥QF,
又BC∩PE=F,∴QF⊥平面PBC,即F是Q点在平面PBC内的射影,
∵F恰好是△PBC的重心,∴
=
,
∵AA1=
,AB=2,∴Q(1,1,0),P(1,1,
),E(1,2,0),设F(a,b,c),
=
=(0,
,-
)=(a-1,b-1,c-
),
∴F(1,
,
),
=(0,
,
),
∵
•
=
-
=0,∴k=
,或k=-
.(舍)
∴当k为
时,Q点在平面PBC内的射影恰好是△PBC的重心.
| 2 |
| 2 |

以D为原点,DA为x轴,DC为y轴,建立空间直角坐标系,
P(1,1,
| 2 |
B(2,2,0),C(0,2,0),
| PA |
| 2 |
| PB |
| 2 |
| PC |
| 2 |
设平面PBC的法向量
| n |
|
取x=1,得
| n |
| 2 |
设直线PA与平面PBC所成角为θ,
sinθ=|cos<
| PA |
| n |
0-
| ||||
|
| ||
| 3 |
∴直线PA与平面PBC所成角的正弦值为
| ||
| 3 |
(Ⅱ)取BC中点E,连结QE,PE,则QE⊥BC,PE⊥BC,
∴BC⊥平面PQE,
过Q作QF⊥PE,交PE于F,∵QF?平面PQE,∴BC⊥QF,
又BC∩PE=F,∴QF⊥平面PBC,即F是Q点在平面PBC内的射影,
∵F恰好是△PBC的重心,∴
| PF |
| 2 |
| 3 |
| PE |
∵AA1=
| 2 |
| k |
| 2 |
| k |
| PF |
| 2 |
| 3 |
| PE |
| 2 |
| 3 |
| 1 |
| 3k |
| 2 |
| k |
∴F(1,
| 5 |
| 3 |
| 5 |
| 3k |
| QF |
| 2 |
| 3 |
| 5 |
| 3k |
∵
| QF |
| PF |
| 4 |
| 9 |
| 5 |
| 9k2 |
| ||
| 2 |
| ||
| 2 |
∴当k为
| ||
| 2 |
点评:本题考查直线PA与平面PBC所成角的正弦值的求法,考查当k为何值时,Q点在平面PBC内的射影恰好是△PBC的重心的求法,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
在△ABC中,A,B,C的对边分别是a,b,c,其中a=
,b=
,sinB=
,则角A的取值一定属于范围( )
| 5 |
| 3 |
| ||
| 2 |
A、(
| ||||||||
B、(
| ||||||||
C、(0,
| ||||||||
D、(
|
已知集合A={x|x-1>0},B={x||x-1|≤2},则A∩B=( )
| A、{x|x≥1} |
| B、{x|-1≤x≤3} |
| C、{x|x≤3} |
| D、{x|1<x≤3} |
以椭圆
+
=1的左焦点为焦点,以坐标原点为顶点的抛物线方程为( )
| x2 |
| 4 |
| y2 |
| 3 |
| A、y2=-4x |
| B、y2=-2x |
| C、y2=-8x |
| D、y=-x |
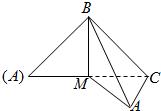 如图,等腰直角△ABC中,已知AB=BC=2,M为AC中点,沿BM将它折成二面角,折后A,C间的距离为
如图,等腰直角△ABC中,已知AB=BC=2,M为AC中点,沿BM将它折成二面角,折后A,C间的距离为 如图是正四面体的平面展开图,M、N、G分别为DE、BE、FE的中点,则在这个正四面体中,MN与CG所成角的大小为
如图是正四面体的平面展开图,M、N、G分别为DE、BE、FE的中点,则在这个正四面体中,MN与CG所成角的大小为