题目内容

已知
a
，
b
为两个非零向量，且
a
=2
b
，（
a
+
b
）⊥
b
，求向量
a
与向量
b
的夹角．
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：直接利用向量的垂直，数量积为0，转化求解向量的夹角即可．
解答： 解：
a
，
b
为两个非零向量，且
a
=2
b
，（
a
+
b
）⊥
b
，
可得（
a
+
b
）•
b
=0
即
a
•
b
+
b
•
b
=0，
可得：|
a
||
b
|cos＜
a
，
b
＞+|
b
|2=0，
∴2|
b
||
b
|cos＜
a
，
b
＞+|
b
|2=0
cos＜
a
，
b
＞=-
1
2
．
∴＜
a
，
b
＞=120°．
向量
a
与向量
b
的夹角为120°．
点评：本题考查向量的数量积与向量的垂直关系的应用，向量的夹角的求法，考查计算能力．
练习册系列答案
相关题目
若函数f（x）=ln
1+x
1-x
+sinx，则关于a的不等式f（a-2）+f（2a-2）＞0的解集是（　　）
A、（-∞，
4
3
）
B、（
1
2
，
4
3
）
C、（
4
3
，
3
2
）
D、（
4
3
，+∞）
（1）已知cosα=
1
5
，求sinα，tanα的值；
（2）已知角α的终边过点P（4a，-3a）（a＜0），求2sinα+cosα的值．
若集合A={y|y=x 
1
5
，-1≤x≤1}，B={y|y=2，0＜x≤1}，则A∩B等于
 
．
设f（x）在R上单调的是奇函数，若f（k•log2t）+f（log2t-log22t-2）＞0，?t＞0恒成立，求实数k的取值范围．
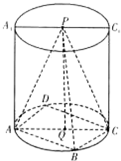如图，已知圆柱的上、下底面圆心分别为P、Q，AA1与CC1是圆柱的母线，正方形ABCD内接于下底面圆Q，AB=kAA1=2，连接PA、PB、PC．
（Ⅰ）当k=
2
时，求直线PA与平面PBC所成角的正弦值；
（Ⅱ）当k为何值时，Q点在平面PBC内的射影恰好是△PBC的重心．
已知各项均不为零的数列{an}的前n项和为Sn，且4Sn=an•an+1+1（n∈N*），其中a1=1．
（1）求证：a1，a3，a5成等差数列；
（2）求证：数列{an}是等差数列；
（3）设数列{bn}满足2bn=1+
1
an
(n∈N*)，且Tn为其前n项和，求证：对任意正整数n，不等式2Tn＞log2an+1恒成立．
已知△ABC三个内角A，B，C的对边分别为a，b，c，2c cosB=2a-
3
b．
（I）求C；
（Ⅱ）若cosB=
2
3
，求cosA的值．
在△ABC中，a、b、c满足a2+b2+c2=ab+bc+ac，则△ABC一定是（　　）
A、等边三角形
B、直角三角形
C、锐角三角形
D、钝角三角形

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网