题目内容
在△ABC中，A，B，C的对边分别是a，b，c，其中a=
，b=
，sinB=
，则角A的取值一定属于范围（ ）
| 5 |
| 3 |
| ||
| 2 |
A、（
| ||||||||
B、（
| ||||||||
C、（0，
| ||||||||
D、（
|
考点：正弦定理
专题：解三角形
分析：利用正弦定理列出关系式，把sinB，a，b的值代入求出sinA的值，利用正弦函数的性质确定出A的范围即可．
解答：
解：∵△ABC中，a=
，b=
，sinB=
，
∴由正弦定理
=
得：sinA=
=
=
＞
，
则A的范围为（
，
）∪（
，
），
故选：D．
| 5 |
| 3 |
| ||
| 2 |
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| asinB |
| b |
| ||||||
|
| ||
| 6 |
| ||
| 2 |
则A的范围为（
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
故选：D．
点评：此题考查了正弦定理，以及正弦函数的性质，熟练掌握正弦定理是解本题的关键．
练习册系列答案
期末好成绩系列答案
99加1领先期末特训卷系列答案
百强名校期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案
金状元绩优好卷系列答案
相关题目
动点P到A（0，2）的距离比它到x轴的距离大2，则动点P的轨迹方程是（ ）
| A、y2=8x |
| B、y2=8x或y=0（x＜0） |
| C、x2=8x |
| D、x2=8x或x=0（y＜0） |
若函数f（x）=ln
+sinx，则关于a的不等式f（a-2）+f（2a-2）＞0的解集是（ ）
| 1+x |
| 1-x |
A、（-∞，
| ||||
B、（
| ||||
C、（
| ||||
D、（
|
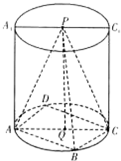如图，已知圆柱的上、下底面圆心分别为P、Q，AA1与CC1是圆柱的母线，正方形ABCD内接于下底面圆Q，AB=kAA1=2，连接PA、PB、PC．