题目内容
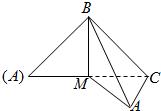 如图,等腰直角△ABC中,已知AB=BC=2,M为AC中点,沿BM将它折成二面角,折后A,C间的距离为
如图,等腰直角△ABC中,已知AB=BC=2,M为AC中点,沿BM将它折成二面角,折后A,C间的距离为| 2 |
考点:二面角的平面角及求法
专题:空间角
分析:由已知得折之后AM=CM=
,AM⊥BM,CM⊥BM,∠AMC是二面角C-BM-A的平面角,由此能求出二面角C-BM-A的大小.
| 2 |
解答:
解:∵等腰直角△ABC中,AB=BC=2,M为AC中点,
∴折之前AC=
=2
,BM⊥AC,
∴折之后AM=CM=
,AM⊥BM,CM⊥BM,
∴∠AMC是二面角C-BM-A的平面角,
∵折后A,C间的距离为
,
∴△AMC是等边三角形,
∴∠AMC=60°,
∴二面角C-BM-A的大小为60°.
故答案为:60°.
∴折之前AC=
| 4+4 |
| 2 |
∴折之后AM=CM=
| 2 |
∴∠AMC是二面角C-BM-A的平面角,
∵折后A,C间的距离为
| 2 |
∴△AMC是等边三角形,
∴∠AMC=60°,
∴二面角C-BM-A的大小为60°.
故答案为:60°.
点评:本题考查二面角的大小的求法,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题中,是平面与平面垂直判定定理的是( )
| A、两个平面相交,如果它们所成的二面角是直二面角,那么两个平面相互垂直 |
| B、如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直 |
| C、如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面 |
| D、如果一个平面内的一条直线垂直于另一平面的两条相交直线,那么这两个平面互相垂直 |
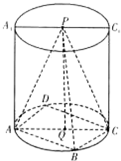 如图,已知圆柱的上、下底面圆心分别为P、Q,AA1与CC1是圆柱的母线,正方形ABCD内接于下底面圆Q,AB=kAA1=2,连接PA、PB、PC.
如图,已知圆柱的上、下底面圆心分别为P、Q,AA1与CC1是圆柱的母线,正方形ABCD内接于下底面圆Q,AB=kAA1=2,连接PA、PB、PC. 在正方体ABCD-A1B1C1D1中,E、F分别为棱D1C1、B1C1的中点,求平面EFC与底面ABCD所成锐二面角的正切值.
在正方体ABCD-A1B1C1D1中,E、F分别为棱D1C1、B1C1的中点,求平面EFC与底面ABCD所成锐二面角的正切值.