题目内容
 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<| π |
| 2 |
(Ⅰ)试确定函数f(x)的解析式;
(Ⅱ)将函数f(x)图象上所有点向左平移
| 1 |
| 4 |
考点:函数y=Asin(ωx+φ)的图象变换,由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(Ⅰ)由函数的图象的顶点坐标求出A,由周期求出ω,由五点法作图求出φ的值,从而求得函数的解析式.
(Ⅱ)由函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,再根据正弦函数的单调性,求得函数g(x)的单调递增区间.
(Ⅱ)由函数y=Asin(ωx+φ)的图象变换规律,求得g(x)的解析式,再根据正弦函数的单调性,求得函数g(x)的单调递增区间.
解答:
解:(Ⅰ)由函数的图象可得A=2,
•
=
-
,求得ω=π.
再根据五点法作图可得π×
+φ=
,∴φ=
.
故函数f(x)的解析式为 f(x)=2sin(πx+
).
(Ⅱ)将函数f(x)图象上所有点向左平移
个单位,
得到函数g(x)=2sin[π(x+
)+
]=2sin(πx+
)的图象.
令 2kπ-
≤πx+
≤kπ+
,k∈z,求得 2k-
≤x≤2k+
,
故函数g(x)的单调递增区间为[2k-
,2k+
],k∈z.
| 1 |
| 4 |
| 2π |
| ω |
| 5 |
| 6 |
| 1 |
| 3 |
再根据五点法作图可得π×
| 1 |
| 3 |
| π |
| 2 |
| π |
| 6 |
故函数f(x)的解析式为 f(x)=2sin(πx+
| π |
| 6 |
(Ⅱ)将函数f(x)图象上所有点向左平移
| 1 |
| 4 |
得到函数g(x)=2sin[π(x+
| 1 |
| 4 |
| π |
| 6 |
| 5π |
| 12 |
令 2kπ-
| π |
| 2 |
| 5π |
| 12 |
| π |
| 2 |
| 11 |
| 12 |
| 1 |
| 12 |
故函数g(x)的单调递增区间为[2k-
| 11 |
| 12 |
| 1 |
| 12 |
点评:本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,函数y=Asin(ωx+φ)的图象变换规律,正弦函数的单调性,属于基础题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,且AD=AB=AA1=2,∠BAD=60°,E为AB的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,且AD=AB=AA1=2,∠BAD=60°,E为AB的中点.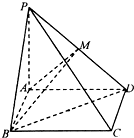 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,点M是PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2,点M是PD的中点.