题目内容
设{an}是首项为1,公差为d的等差数列(d≠0),其前n项的和为Sn.记bn=
,n∈N*,其中c为实数.
(1)若数列{bn}是等差数列,求c的值.
(2)若c=0,且b1,b2,b4成等比数列,证明:
+
+…+
<
.
| nSn |
| n2+c |
(1)若数列{bn}是等差数列,求c的值.
(2)若c=0,且b1,b2,b4成等比数列,证明:
| 1 |
| a1b1 |
| 1 |
| a2b2 |
| 1 |
| anbn |
| 3 |
| 2 |
考点:数列与不等式的综合,等差数列的性质
专题:综合题,等差数列与等比数列
分析:(1)设bn=an+b,根据{an}是首项为1,公差为d的等差数列(d≠0),bn=
,建立方程组,即可求c的值.
(2)求出数列的通项,利用放缩,再裂项求和,即可证明结论.
| nSn |
| n2+c |
(2)求出数列的通项,利用放缩,再裂项求和,即可证明结论.
解答:
(1)解:∵数列{bn}是等差数列,∴设bn=an+b,
∵{an}是首项为1,公差为d的等差数列(d≠0),bn=
,
∴
=an+b,
∴
n3+(1-
)n2=an3+bn2+cn+bc,
∴
,
若c≠0,则a=b=0,∴
矛盾,
∴c=0…(6分)
(2)证明:∵bn=
=1+
d
又b1,b2,b4成等比数列,
∴(1+
)2=1+
d,
∴d=2,
∴an=2n-1,bn=n
∴
+
+…+
=
+
+…+
<1+
(
+
+…+
=1+
(1-
)=
-
<
.…(13分)
∵{an}是首项为1,公差为d的等差数列(d≠0),bn=
| nSn |
| n2+c |
∴
n2+
| ||
| n2+c |
∴
| d |
| 2 |
| d |
| 2 |
∴
|
若c≠0,则a=b=0,∴
|
∴c=0…(6分)
(2)证明:∵bn=
| Sn |
| n |
| n-1 |
| 2 |
又b1,b2,b4成等比数列,
∴(1+
| d |
| 2 |
| 3 |
| 2 |
∴d=2,
∴an=2n-1,bn=n
∴
| 1 |
| a1b1 |
| 1 |
| a2b2 |
| 1 |
| anbn |
| 1 |
| 1×1 |
| 1 |
| 2×3 |
| 1 |
| n(2n-1) |
| 1 |
| 2 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| n(n-1) |
=1+
| 1 |
| 2 |
| 1 |
| n |
| 3 |
| 2 |
| 1 |
| 2n |
| 3 |
| 2 |
点评:本题考查数列与不等式的综合,考查数列的通项,考查放缩、裂项法求和,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
一只昆虫在边长分别为6,8,10的三角形区域内随机爬行,则其到三角形顶点的距离小于2的地方的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设a,b,c均为正数,且(
)a=log2a,(
)b=log
b,2c=log
c,则a,b,c的大小关系是( )
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| A、a<b<c |
| B、c<b<a |
| C、c<a<b |
| D、b<a<c |
等差数列{an}满足a7+a8+a3=15,函数fn(x)=sin(
x+
),那么f5(a6)的值为( )
| π |
| n |
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
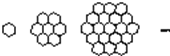 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n个图的蜂巢总数.
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,以f(n)表示第n个图的蜂巢总数.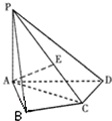 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点. 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<