题目内容
已知左焦点为
的椭圆过点
．过点
分别作斜率为
的椭圆的动弦
，设
分别为线段的中点．
（1）求椭圆的标准方程；
（2）若
为线段
的中点，求
；
（3）若
，求证直线
恒过定点，并求出定点坐标．
解 （1）由题意知
设右焦点
椭圆方程为
（2）设
则 
① 
②
②-①，可得
（3）由题意
，设
直线
，即
代入椭圆方程并化简得
同理
当
时， 直线的斜率
直线的方程为
又
化简得
此时直线过定点（0，
）
当
时，直线即为
轴，也过点（0，）
综上，直线过定点（0，）
练习册系列答案
相关题目
的一个焦点，则m= . 
的值域为
，则
的最小值为 .
且函数
的零点均在区间
内，圆
的面积的最小值是（ ）
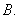
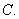
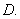
是圆
的直径
是圆
，
，
，
= ．
，
的夹角为
，
，若
，则
___（ ）
－
＝1(a＞0，b＞0)的右焦点F作与x轴垂直的直线，分别与双曲线、双曲线的渐近线交于点M、N(均在第一象限内)，若
＝4
，则双曲线的离心率为 
为抛物线
上的动弦，且
, 则弦
到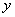
轴的最小距离
C. 1 D. 
、
，则线段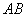
的垂直平分线的方程是 
B．
D．