题目内容

12．已知正数组成的等比数列{an}，若a1•a20=100，那么a7+a14的最小值为20．

分析 利用正数组成的等比数列{an}的性质可得：a1•a20=100=a7a14，再利用基本不等式的性质即可得出．

解答 解：∵正数组成的等比数列{an}，∵a1•a20=100，
∴a1•a20=100=a7a14，
那么a7+a14≥2$\sqrt{{a}_{7}{a}_{14}}$=20，当且仅当a7=a14时取等号．
∴a7+a14的最小值为20．
故答案为：20．

点评 本题考查了基本不等式的性质、等比数列的性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
2．已知函数f（x）的定义域为R，且f（x）=$\left\{\begin{array}{l}{{x}^{2}+2，x∈[0，1]}\\{2-{x}^{2}，x∈（-1，0）}\end{array}\right.$，f（x+1）=f（x-1），则方程f（x）=$\frac{2x+1}{x}$在区间[3，-3]上的所有实根之和为（　　）
A．-8B．-2C．1D．8
3．已知正实数m，若x10=a0+a1（m-x）+a2（m-x）2+…+a10（m-x）10，其中a8=180，则m值为（　　）
A．4B．2C．3D．6
20．已知两条直线l1：（m+3）x+4y+3m-5=0，l2：2x+（m+6）y-8=0，且l1⊥l2，则直线l1的一个方向向量是（　　）
A．（1，-$\frac{1}{2}$）B．（-1，-$\frac{1}{2}$）C．（1，-1）D．（-1，-1）
7．已知{an}为等差数列，若a3+a8=24，则a5+a6=（　　）
A．24B．27C．15D．54
17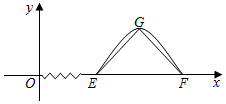．已知函数f（x）=Asinωx（A＞0，ω＞0）的部分图象如图所示，若△EFG是以G为顶点，EF为底边且长为4的等腰直角三角形，则f（100）=（　　）
A．0B．1C．$\sqrt{2}$D．$\sqrt{3}$
4．在数列{an}中，已知an+1-an=1，a2是a1与a4的等比中项
（1）求数列{an}的通项公式；
（2）设Sn是数列{an}的前n项和，记T2n=-S1+S2-S3+…+（-1）2nS2n，求T2n．
1．在△ABC中，D是BC的中点，若$\overrightarrow{AD}=λ（\overrightarrow{AB}+\overrightarrow{AC}）$，则λ=$\frac{1}{2}$．
2．若A={x|x=4k+1，k∈Z}，B={x|x=2k-1，k∈Z}，则（　　）
A．A⊆BB．B⊆AC．A=BD．A∩B=∅

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网